Что называют простыми механизмами
Умение облегчать себе труд с помощью технологий отличает человека от животного. Тысячи лет назад наши предки научились мастерить простые механизмы, которые способны увеличивать усилие, а также изменять направление прикладываемой силы. Принципы их работы лежат в основе любого орудия труда — от садовой лопаты до подъёмного крана. Простые механизмы — приспособления, служащие для преобразования вектора силы по величине и/или направлению.
Виды простых механизмов
Существует несколько видов простых механизмов:
- наклонная плоскость и её разновидности: клин и винт;
- рычаг и его разновидности: блок и ворот.
Теперь расскажем, как они работают. В этой статье мы рассмотрим действие идеальных механизмов, в работе которых не учитывается сила трения.
Как простые механизмы облегчают работу
Основной принцип действия простых механизмов — это преобразование силы и изменение направления её приложения.
Хотя простые механизмы не создают энергию, они позволяют более эффективно расходовать силу, перераспределяя её по направлениям и увеличивая плечи приложения. Комбинируя простые механизмы, получают сложные машины. Например, велосипед сочетает рычаги (педали), блоки (передачу цепи и шестерни), колесо и ось.
Вот основные способы, с помощью которых простейшие механизмы облегчают труд:
- Увеличение силы (механическое преимущество). Механизмы, такие как рычаг или подвижный блок, позволяют увеличить выходную силу. Это означает, что при приложении меньшего усилия можно поднять или сдвинуть тяжёлый груз. Например, с помощью длинного рычага можно легко приподнять тяжёлый камень, который не сдвинуть руками.
- Изменение направления силы. Некоторые механизмы (например, неподвижный блок) не уменьшают усилие, но позволяют действовать в более удобном направлении. Например, при подъёме груза на крышу легче тянуть верёвку вниз, используя собственный вес, чем поднимать её вверх руками.
- Увеличение расстояния, уменьшая силу. Механизмы, как наклонная плоскость или винт, позволяют преодолеть сопротивление не за счёт силы, а за счёт расстояния. Груз поднимается медленнее, но усилие требуется меньшее. Это удобно, когда важна точность и экономия сил.
- Преобразование движения. Механизмы могут преобразовывать один вид движения в другой — вращательное в поступательное, прямолинейное в круговое и т.д. Это позволяет лучше управлять рабочим процессом. Например, винт превращает вращение отвёртки в поступательное движение крепёжной детали.
- Повышение точности и контроля. С помощью простых механизмов можно точнее контролировать движение или силу. Клин позволяет аккуратно расколоть древесину по нужной линии, а шестерёнки — плавно и точно передать крутящий момент.
Наклонная плоскость
Подниматься по пологому склону горы легче, чем карабкаться по отвесной скале. Чем меньше наклон — тем легче его преодолеть. Это нехитрое наблюдение помогло людям создать простой механизм — наклонную плоскость.
Допустим, нам нужно поднять груз на определённую высоту. Конечно, можно сделать это непосредственно.

Правда, если груз большой, приложить достаточную силу будет нелегко. Но если поставить его на лёгкую тележку и вкатывать по наклонной плоскости, то понадобится гораздо меньше усилий.

Чем меньше угол наклона плоскости, тем больше выигрыш в силе:
k = l / h
Чтобы просто поднять груз весом в один килограмм, требуется усилие:
F1 = mg = 9,8 H
Теперь посмотрим, какое усилие понадобится, чтобы поднять этот груз на один метр, используя наклонную плоскость длиной десять метров:
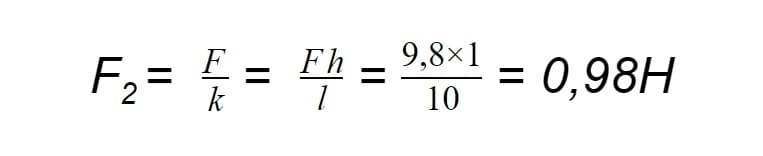
Использование наклонной плоскости позволило нам выиграть в силе в десять раз. Но путь, который нам пришлось пройти с грузом, также увеличился вдесятеро.
Клин
С помощью наклонной плоскости удобно не только поднимать грузы. Рассмотрим топор: его лезвие — это клин, боковые поверхности которого сходятся под острым углом, образуя наклонные плоскости. Когда мы вонзаем топор в полено, эти плоскости с огромной силой раздвигают волокна древесины и заставляют полено расколоться.
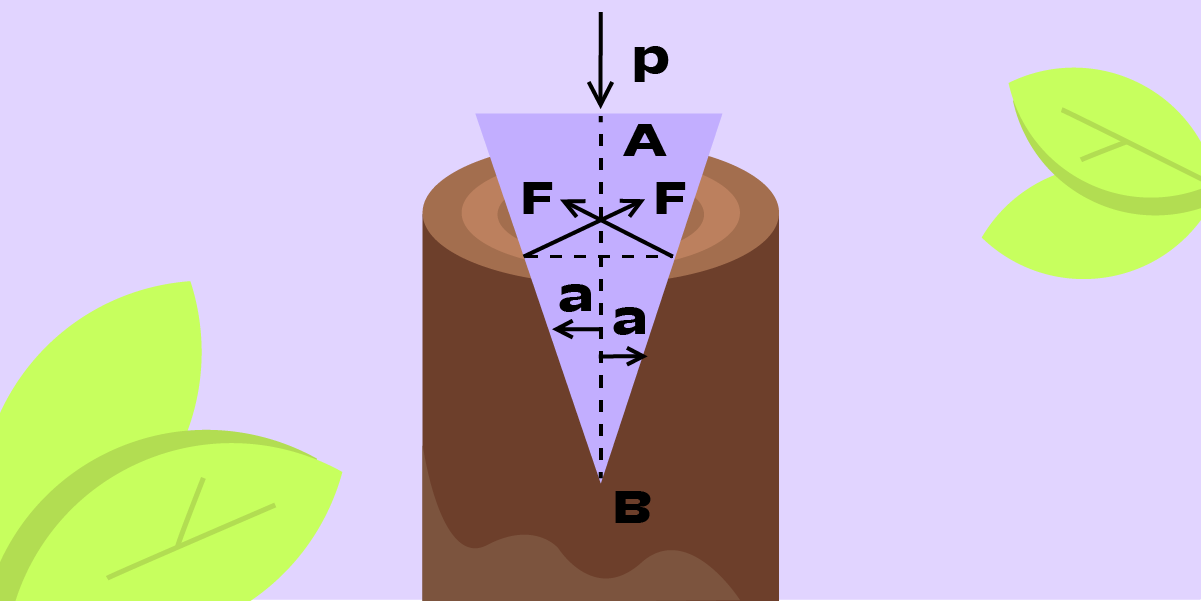
При ударе сила P вгоняет топор в дерево, и на его лезвие действуют сдавливающие силы F со стороны полена. Проекция каждой из сил F на плоскость симметрии лезвия (AB) равна Fsinα.
Поскольку они действуют с двух сторон, условие равновесия сил таково:
P = 2Fsinα
Чем длиннее и острее клин (то есть чем меньше угол), тем меньше может быть P по отношению к 2F. Угол лезвия обычного колуна — около 25°, соответственно, сила Р примерно в пять раз меньше, чем 2F. Иными словами, чтобы расколоть полено, нужно приложить в пять раз меньше усилий, чем требуется, чтобы разорвать его.
Люди пользуются топорами уже более 9 тысяч лет. Гвозди, иглы и ножи работают по тому же принципу.
Клин придуман не человеком, а самой природой: например, клюв дятла легко вонзается в дерево благодаря оптимальной клиновидной форме.
Винт
Если свернуть наклонную плоскость в спираль вокруг цилиндра — получится винт

Впервые описание винта встречается в работах древнегреческого учёного Архита Тарентского, жившего в V–IV веках до нашей эры. Знаменитый Архимед в III веке до нашей эры создал с помощью винта устройство для подъёма воды в оросительные каналы. Винты широко используют для крепления деталей, бурения отверстий и даже в качестве движителя сверхпроходимых шнекороторных вездеходов.
Резьба винта — это наклонная плоскость длиной l и высотой h, свёрнутая в трубочку. Когда мы наворачиваем гайку на болт, мы перемещаем её по наклонной плоскости.
Как и в случае с обычной плоскостью, выигрыш в силе равен отношению h к l, но теперь l рассчитывается по формуле длины окружности:
l = πD
Расстояние между витками называют шагом резьбы. Чем оно меньше, тем длиннее плоскость и больше выигрыш в силе.
Рычаг
Простейший рычаг — это палка, способная вращаться вокруг неподвижной опоры
Принцип рычага используется при работе башенного крана, рычажных весов, кухонных ножниц и даже обычной лопаты. Интересно, что кости в наших конечностях тоже работают как рычаги.
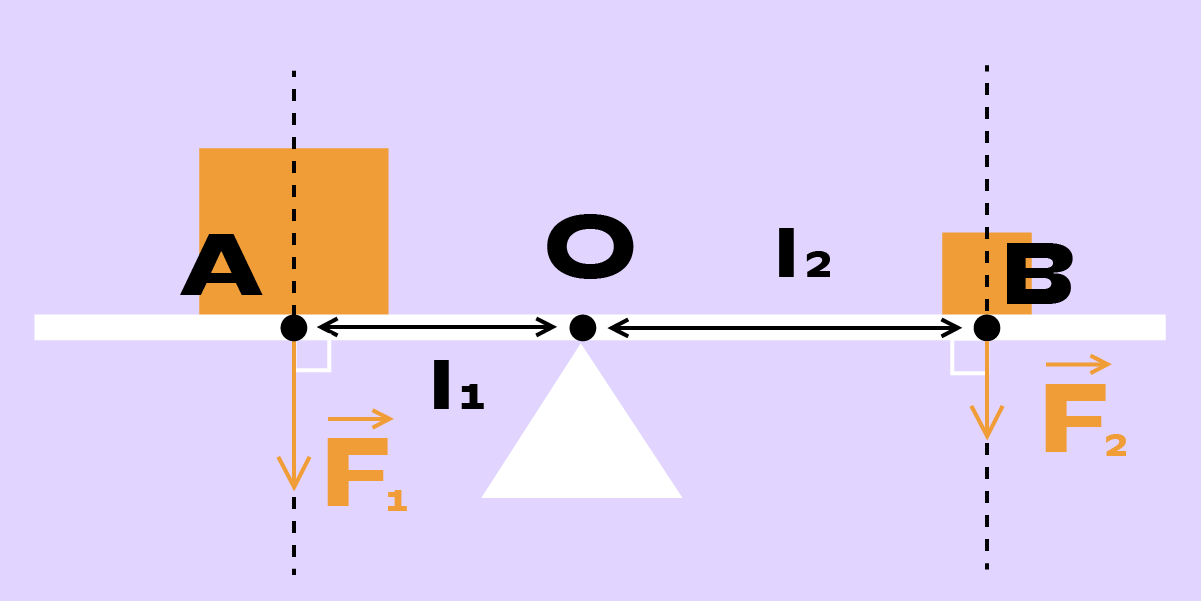
У любого рычага есть точка опоры (О) и два плеча (длины l1 и l2), к которым в точках A и B прикладываются силы.
Вращение рычага зависит от приложенной к нему силы и от длины плеча. Чем больше сила и чем длиннее плечо, тем сильнее вращающее действие. Именно поэтому работать лопатой проще, держа её ближе к концу черенка, а нести груз на согнутой руке легче, чем на вытянутой.

На рисунке тело А воздействует на рычаг с большей силой, чем тело B, но плечо l1 короче, чем l2, поэтому тела находятся в равновесии. В таких случаях говорят, что моменты двух сил уравновешены.
Момент силы — произведение силы на длину плеча:
M = F ⋅ l
Рассчитаем моменты силы для обоих тел:
MA = PA ⋅ l1 = mAgl1
MB = PB ⋅ l2 = mBgl2
Тела находятся в равновесии, значит:
mAgl1 = mBgl2
Чем больше будет длина плеча l2, тем меньшее усилие понадобится, чтобы уравновесить тело A. Так, при достаточной длине рычага можно поднять даже неподъёмный груз.
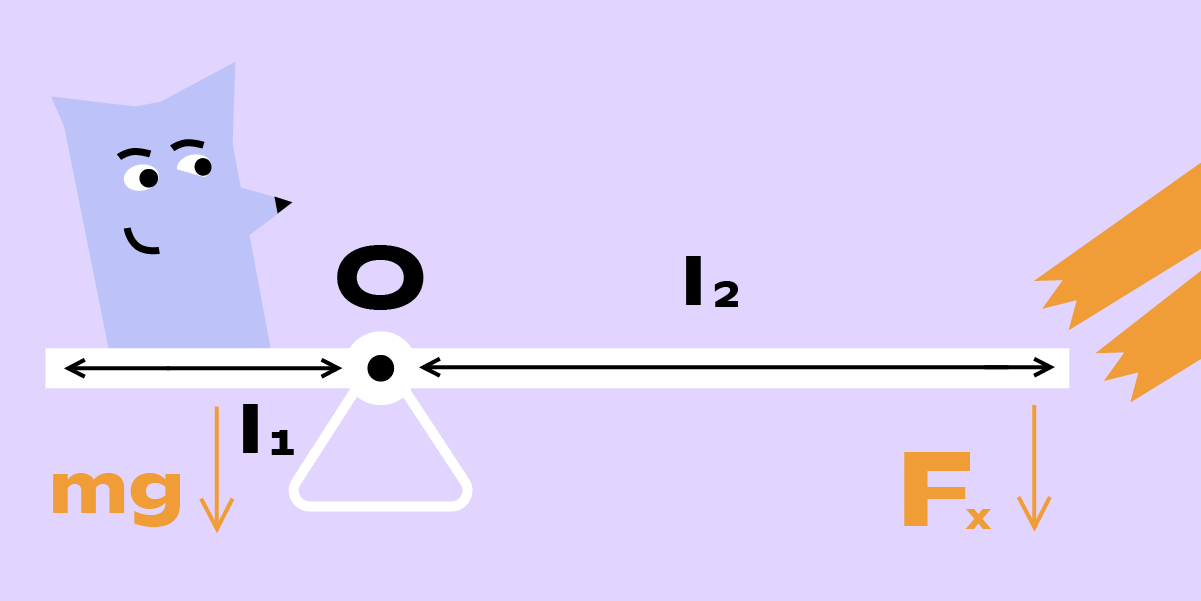
Чтобы просто поднять тело, нужно преодолеть силу тяжести:
F = mg
Чтобы вычислить силу для поднятия тела рычагом, нужно приравнять соответствующие моменты сил:
mgl1 = Fx ∙ l2
Следовательно,
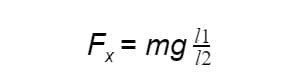
Если l1 больше l2 в пять раз, то:
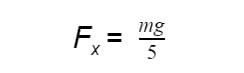
Увеличивая длину плеча, мы выигрываем в силе, но проигрываем в перемещении. Нам удалось уменьшить силу в пять раз, но чтобы короткое плечо рычага поднялось на 10 сантиметров вверх, придётся опустить длинное на 50 сантиметров.
Блок
Частный случай рычага — блок.
Блок это — колесо с жёлобом, в который вложен трос
Если ось колеса зафиксировать, к одному концу троса привязать груз, а за другой тянуть, получится простой механизм — неподвижный блок.

На груз действует сила тяжести F = mg. Чтобы удержать верёвку, требуется приложить такую же силу. Никакого выигрыша в величине силы неподвижный блок не даёт. Зато можно менять её направление — тянуть верёвку в любую сторону.
Если прицепить груз к оси колеса, один конец верёвки закрепить, а за другой тянуть, получится подвижный блок, который позволяет выиграть в силе в два раза.
Эффект достигается за счёт того, что блок с грузом поднимают как бы сразу две верёвки: за левую тянет человек, а правую натягивает вбитый в потолок гвоздь.

За выигрыш в силе приходится платить проигрышем в перемещении: чтобы поднять груз на нужную высоту h, понадобится выбрать вдвое большую длину и верёвки:
l = 2h
Ворот
Ворот издревле применяется для поднятия воды из колодца.
К барабану, способному вращаться вокруг своей оси, прикреплены верёвка и рукоять. Когда мы вращаем рукоятку — вращается и цилиндр, а верёвка наматывается на него, поднимая или опуская груз
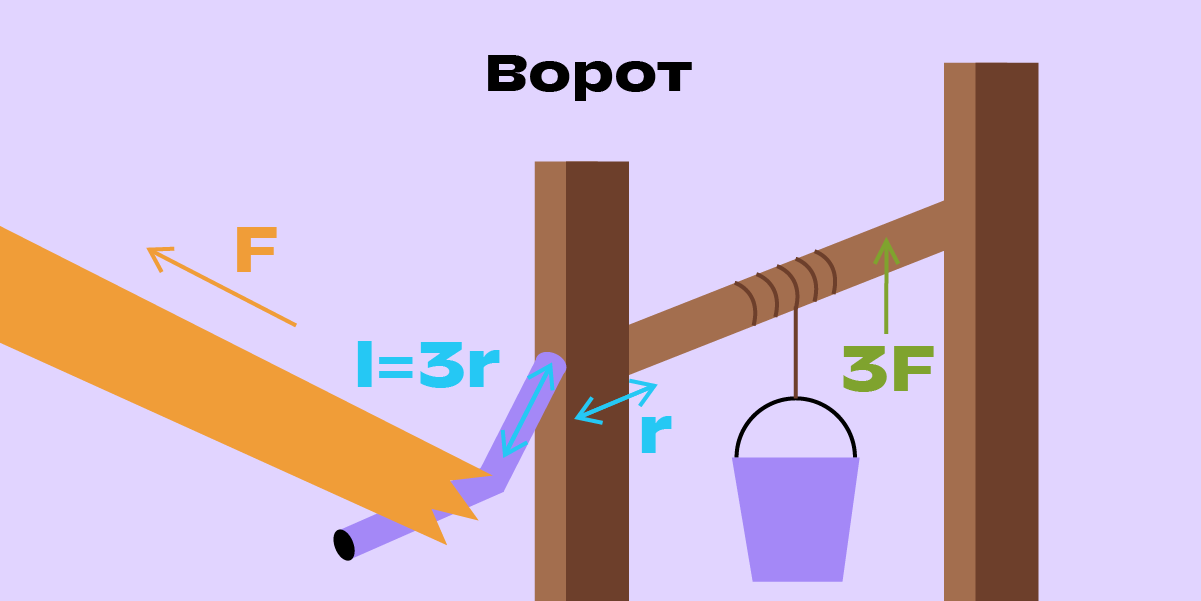
Ворот действует по тому же принципу, что и рычаг: плечом силы в данном случае становится рукоятка, а плечом груза — радиус барабана. Чем длиннее рукоять относительно радиуса барабана — тем больше выигрыш в силе.
На рисунке длина рукояти равна трём радиусам барабана. Значит, он поднимает ведро с силой, в три раза большей, чем сила наших рук. При этом путь, который проходит рукоять ворота, в три раза длиннее куска верёвки, который в это время накручивается на вал.
| Вид простого механизма | Подвид простого механизма | Суть |
| Наклонная плоскость и её разновидности | Наклонная плоскость | Плоскость, установленная под углом к горизонтальной поверхности |
| Клин | Объект боковые поверхности которого сходятся под острым углом, образуя наклонные плоскости | |
| Винт | Свёрнутая наклонная плоскость в спираль вокруг цилиндра | |
| Рычаг и его разновидности | Рычаг | Палка, способная вращаться вокруг неподвижной опоры |
| Блок | Колесо с жёлобом, в который вложен трос | |
| Ворот | К барабану, способному вращаться вокруг своей оси, прикреплены верёвка и рукоять. Когда мы вращаем рукоятку — вращается и цилиндр, а верёвка наматывается на него, поднимая или опуская груз |
Золотое правило механики
Все рассмотренные примеры простых механизмов имеют одно общее свойство, которое называют золотым правилом механики.
Во сколько раз мы выигрываем в силе, во столько же раз проигрываем в перемещении
Произведение силы на перемещение в механике называется работой и обозначается буквой А:
A = F ⋅ S ⋅ cos α
где α — угол между векторами силы и перемещения.
Если направления векторов совпадают, формула работы выглядит проще:
A = F ⋅ S
Сэкономить в силе больше, чем проиграть в перемещении — то есть выиграть в работе — не позволяет ни один механизм. Чем меньше силы нужно потратить при подъёме тела по наклонной плоскости, тем длиннее должна быть эта плоскость. Чем меньше сил нужно для воздействия на рычаг — тем длиннее должно быть его плечо.
«Дайте мне точку опоры, и я переверну Землю» — заявил Архимед. Теоретически он мог бы поднять груз, равный нашей планете, выбрав рычаг подходящей длины. Масса Земли — примерно 6 000 000 000 000 000 000 000 тонн, в то время как человек в среднем способен поднять груз около 60 килограммов. А значит, плечо силы должно быть больше плеча груза в 100 000 000 000 000 000 000 000 раз. Поэтому, чтобы плечо груза сдвинулось хотя бы на один сантиметр, учёному пришлось бы сдвинуть плечо силы на 1000 000 000 000 000 000 км. Даже со скоростью движения в 1 м/с на это ушло бы тридцать тысяч миллиардов лет.
Ответим на ваши вопросы
Свяжемся с вами в течение 5 минут и проведём бесплатную консультацию по вопросам перехода на домашнее обучение
Позвоним с 8 до 21 в рабочие дни






