Понятие перпендикулярных прямых
Перпендикулярные прямые — это две прямые одной плоскости, которые пересекаются под углом 90° и образуют 4 прямых угла.
Начнём с самого начала — углы бывают острые, прямые и тупые.
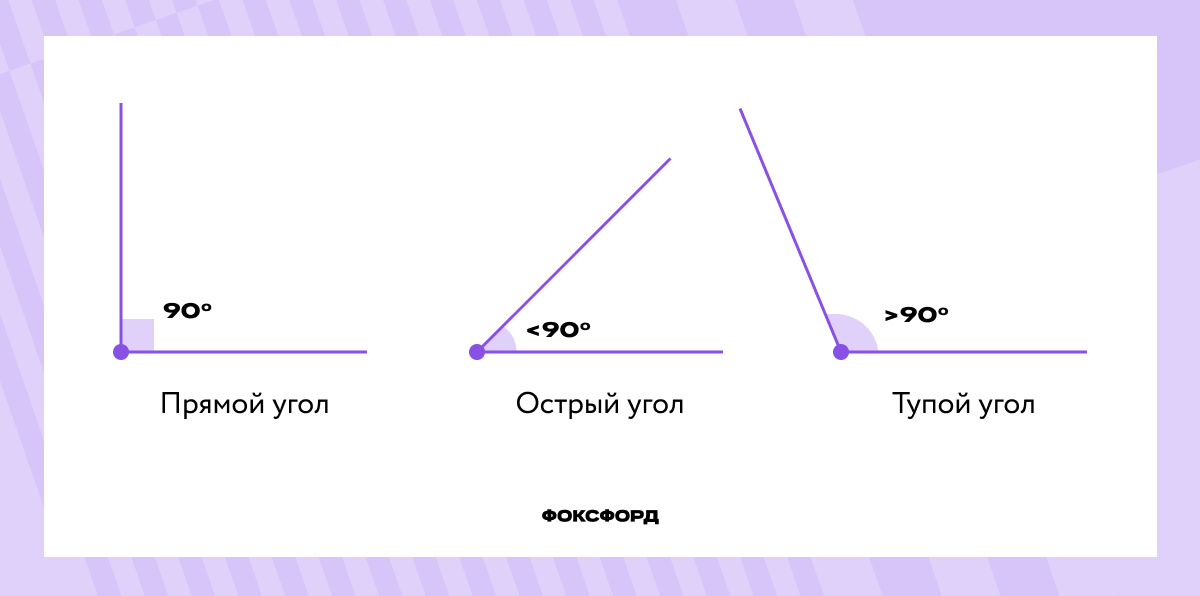
Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развёрнутым. Два угла с одной общей стороной называются смежными.
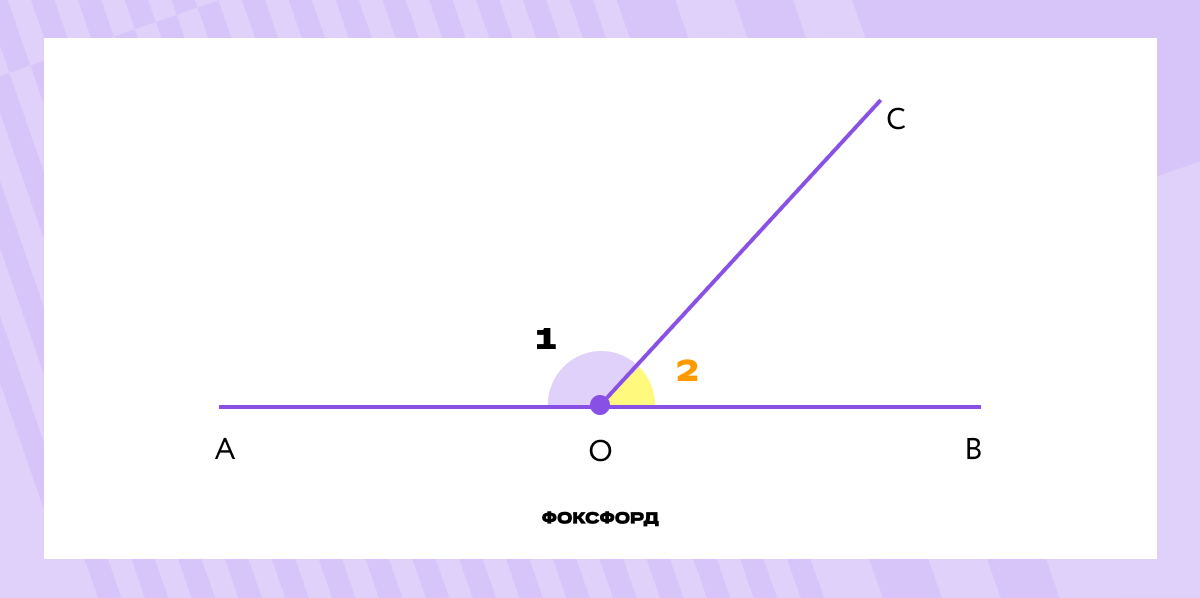
На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2. Сумма смежных углов составляет 180°.
Поэтому если один из смежных углов прямой, то второй также оказывается прямым:
180° – 90° = 90°
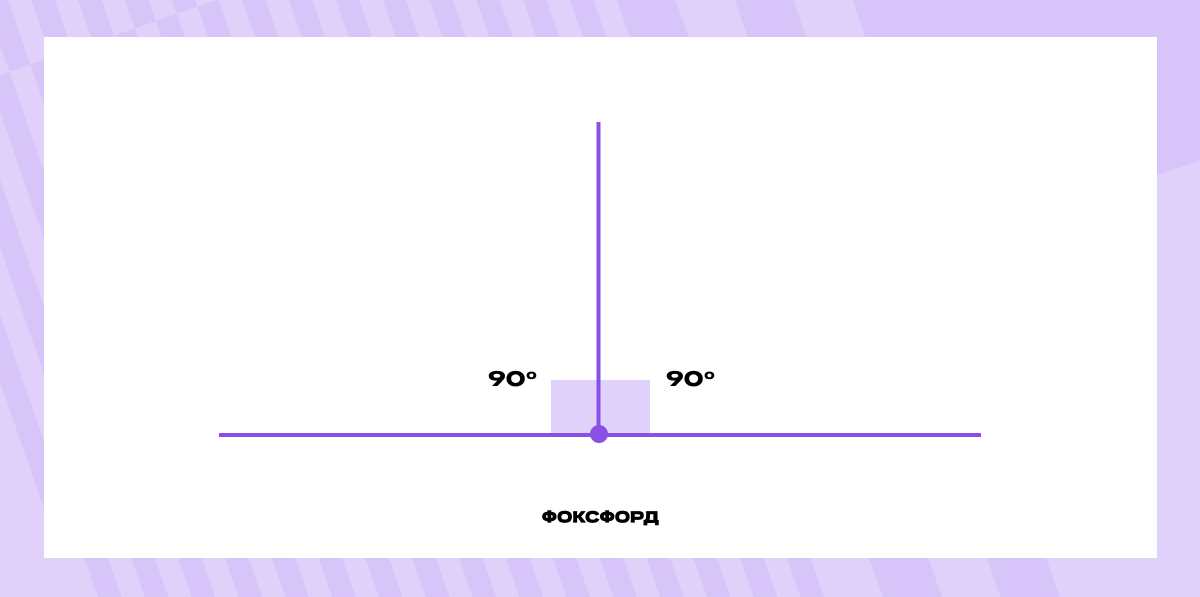
При пересечении двух прямых образуются четыре угла.
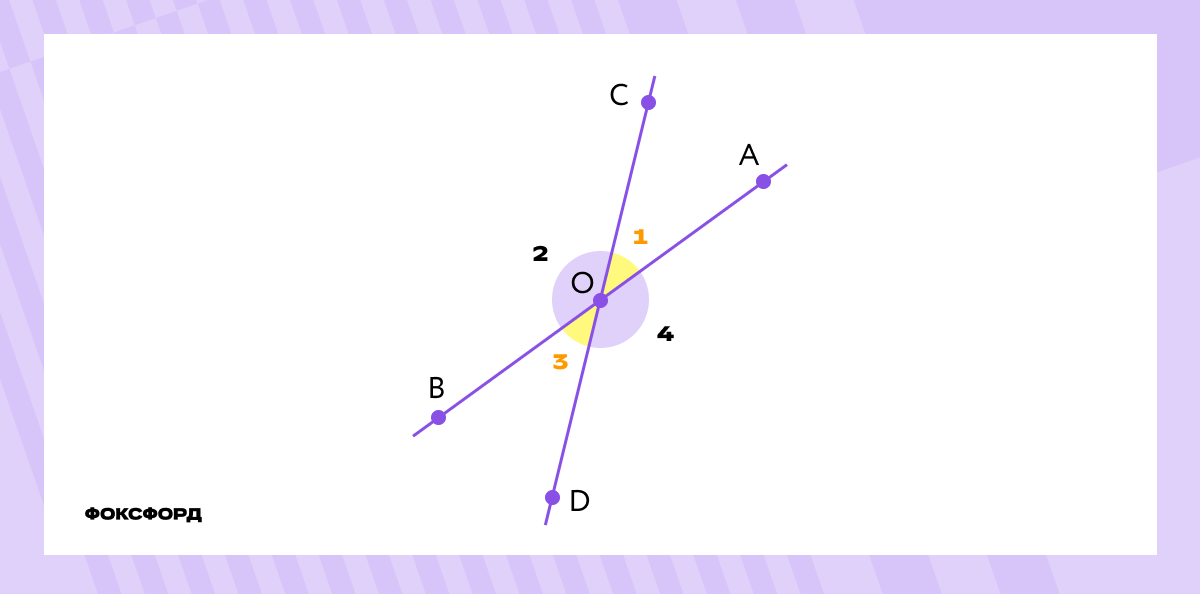
Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.
∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:
∡1 + ∡2 = 180°
∡1 + ∡4 = 180°
∡2 = ∡4
То же справедливо и для ∡1 и ∡3. Вертикальные углы равны.
Две прямые на плоскости называются перпендикулярными, если они пересекаются под прямым углом.
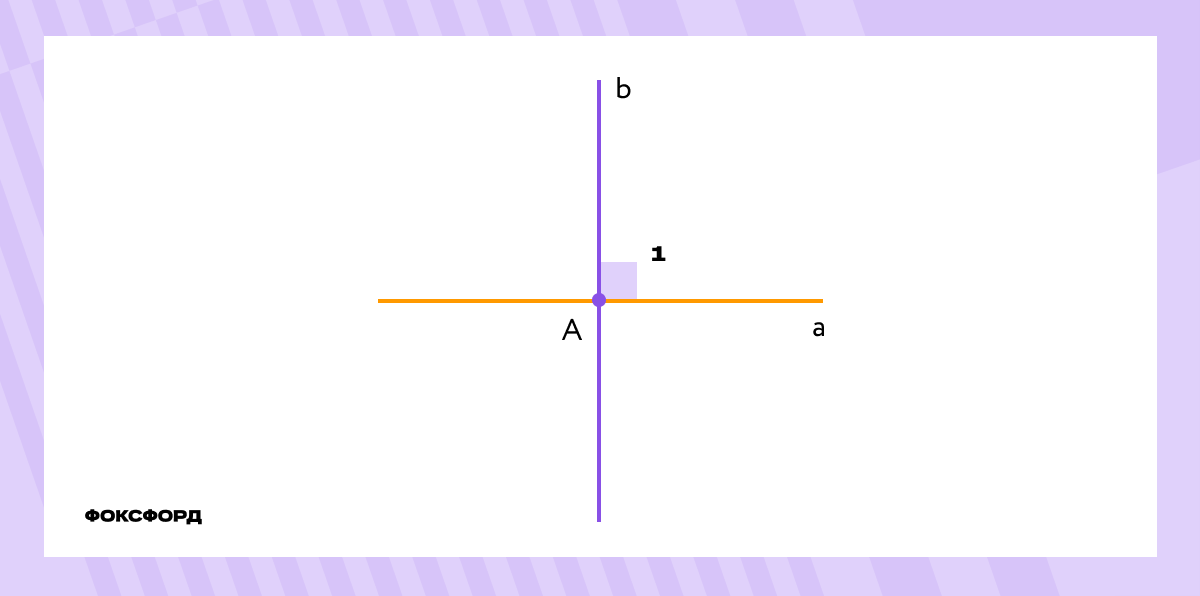
∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.
Перпендикулярность прямых принято обозначать так: a⟂b.
Как построить перпендикулярные прямые
Разберём несколько доступных способов построить перпендикулярные прямые.
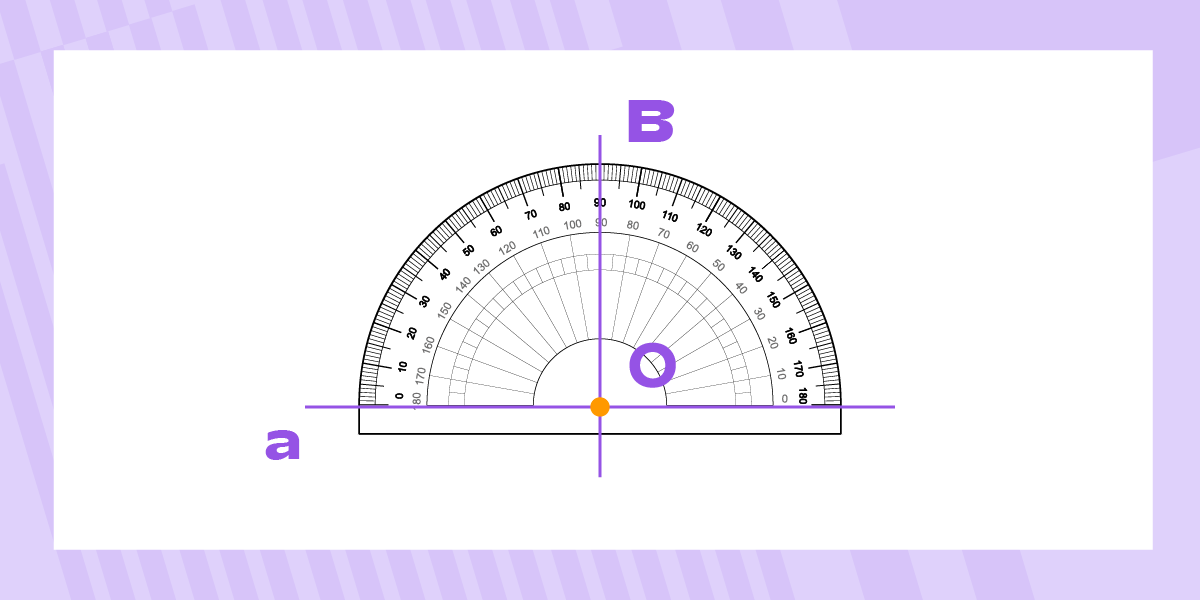
Построение перпендикулярных прямых при помощи транспортира
Инструменты: транспортир, линейка, карандаш, бумага
- Сначала проведите прямую линию — это будет прямая a.
- Выберите любую точку на этой прямой. Обозначим её как O. Именно из этой точки мы будем строить перпендикуляр.
- Поместите центр транспортира точно на точку O.
- Совместите основание транспортира (линию 0–180°) с прямой a.
- На шкале транспортира отметьте точку, соответствующую 90° от прямой.
- Поставьте точку в направлении 90° от точки O. Пусть это будет точка B.
- Соедините с помощью линейки точку O с новой точкой B — получится вторая прямая.
- Вы получили две перпендикулярные прямые, пересекающиеся под прямым углом (90°).
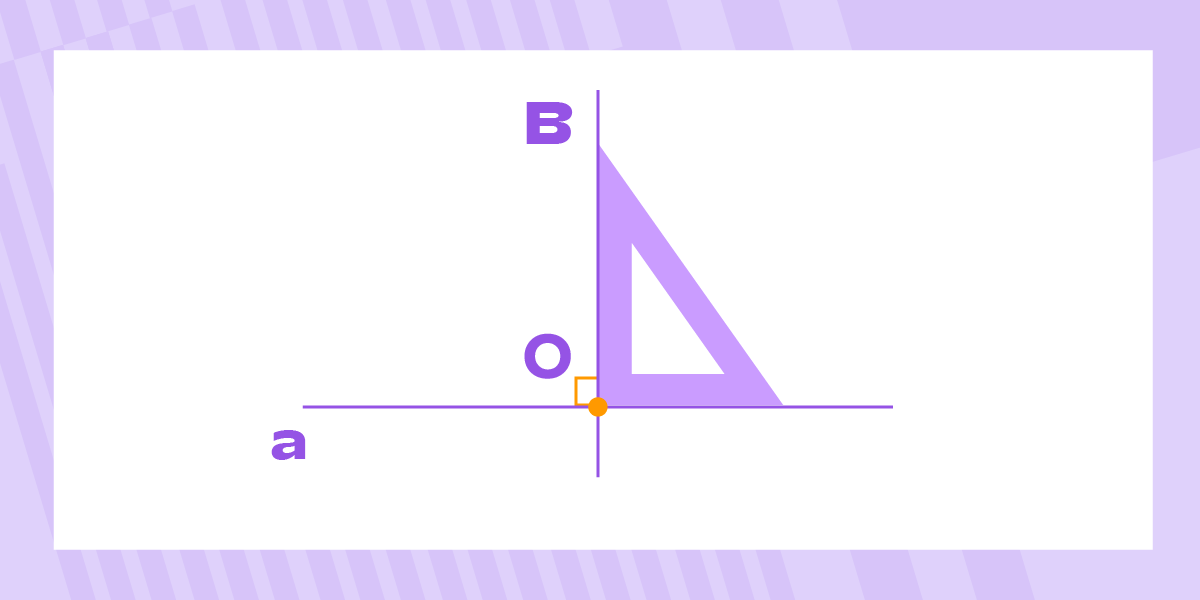
Построение перпендикулярных прямых при помощи угольника
Инструменты: угольник, линейка, карандаш, бумага
- Проведите прямую линию с помощью линейки — это будет прямая a.
- Отметьте точку O на прямой a — из этой точки будет выходить перпендикулярная прямая.
- Поставьте угольник так, чтобы один его катет (прямая сторона) совпадал с прямой a.
- Убедитесь, что вершина прямого угла точно совпадает с точкой O.
- По другому катету угольника проведите линию, начиная из точки O новую точку B.
- Эта линия будет перпендикулярна исходной прямой, поскольку построена под прямым углом (90°).
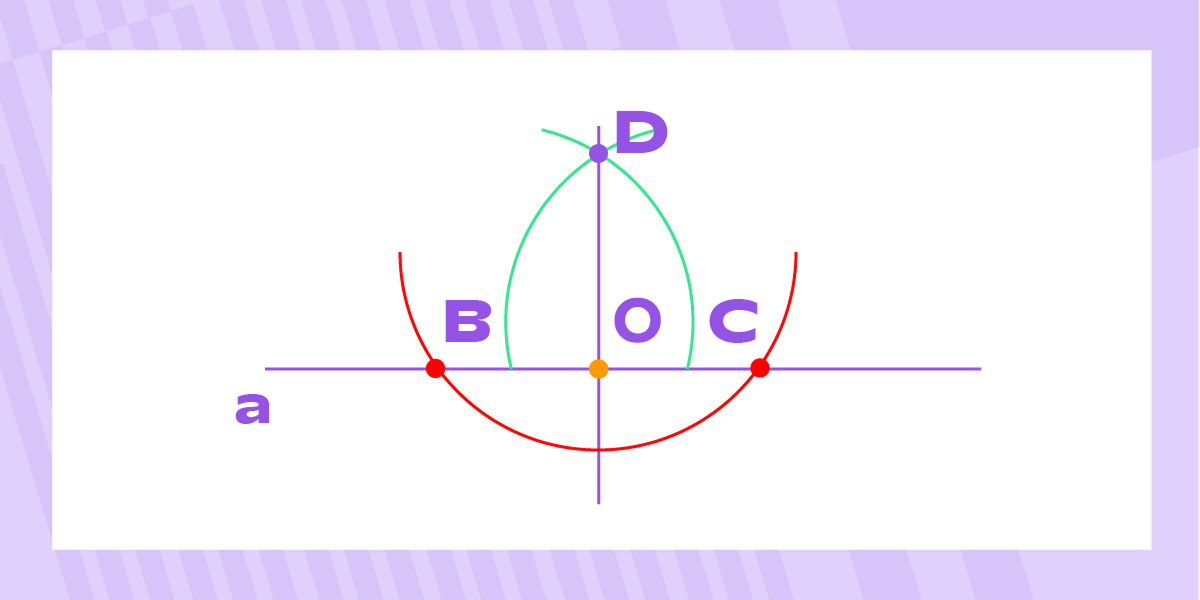
Построение перпендикулярных прямых при помощи циркуля
Инструменты: циркуль, линейка, карандаш, бумага
- Проведите прямую линию с помощью линейки — это будет прямая a.
- Отметьте точку O на прямой a — из этой точки будет выходить перпендикулярная прямая.
- Поставьте иглу циркуля в точку O.
- Нарисуйте дугу, пересекающую прямую a в двух точках.
- Обозначим их как B и C. Они должны быть по разные стороны от точки O на одинаковом расстоянии.
- Не меняя радиус циркуля, поставьте иглу в точку B и нарисуйте дугу выше прямой.
- Перенесите иглу в точку C и нарисуйте такую же дугу.
- Эти две дуги пересекутся в точке D — она будет расположена строго над точкой O.
- Соедините точки O и D прямой линией.
- Линия OD будет перпендикулярна прямой a и проходить через заданную точку O.
Теорема о перпендикулярных прямых
Теорема о перпендикулярных прямых звучит следующим образом:
Через каждую точку прямой можно провести перпендикулярную ей прямую, притом только одну. Это свойство — единственность перпендикуляра в данной точке — лежит в основе многих построений и доказательств в геометрии.
Доказательство теоремы о перпендикулярных прямых
Построим доказательство теоремы о перпендикулярных прямых от противного, то есть для начала предположим, что утверждение неверно.
Возьмём прямую a, отметим на ней точки О и B. От луча OB отложим ∡BOA = 90°. Таким образом, отрезок OA будет находиться на прямой, перпендикулярной а.
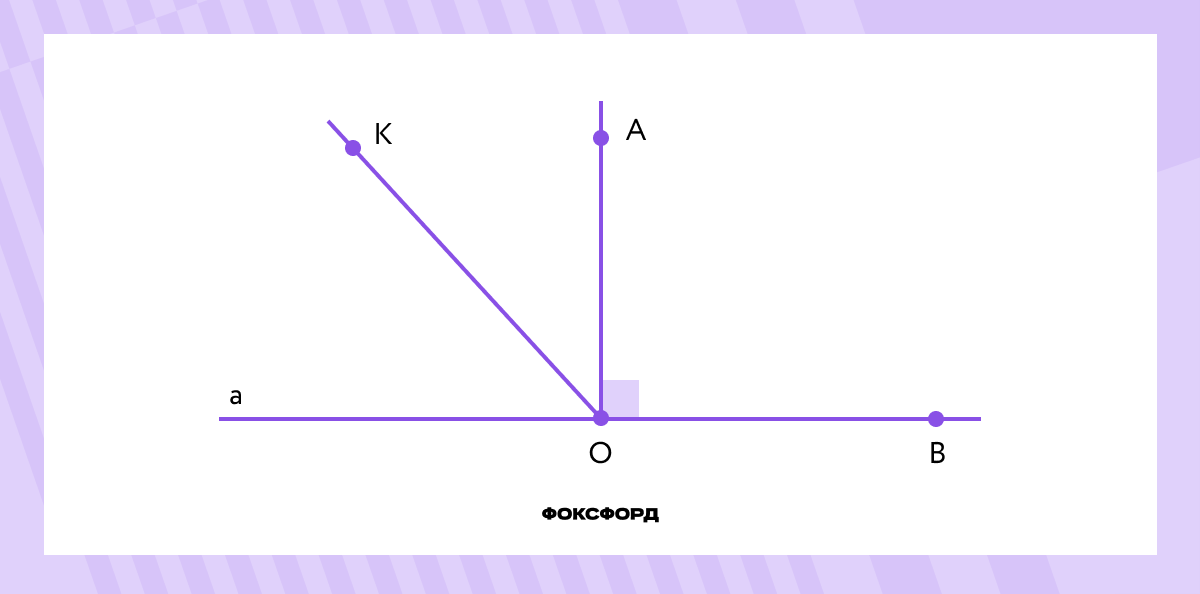
Теперь предположим, что в той же полуплоскости существует другой перпендикуляр к а, проходящий через О. Назовём его OK. ∡BOK и ∡BOA равны 90° и лежат в одной полуплоскости относительно луча OB. Но от луча OB в данной полуплоскости можно отложить только один прямой угол. Поэтому другой прямой, проходящей через О и перпендикулярной a, не существует. Теорема доказана.
Свойство перпендикулярных прямых
Две прямые, перпендикулярные третьей, не пересекаются
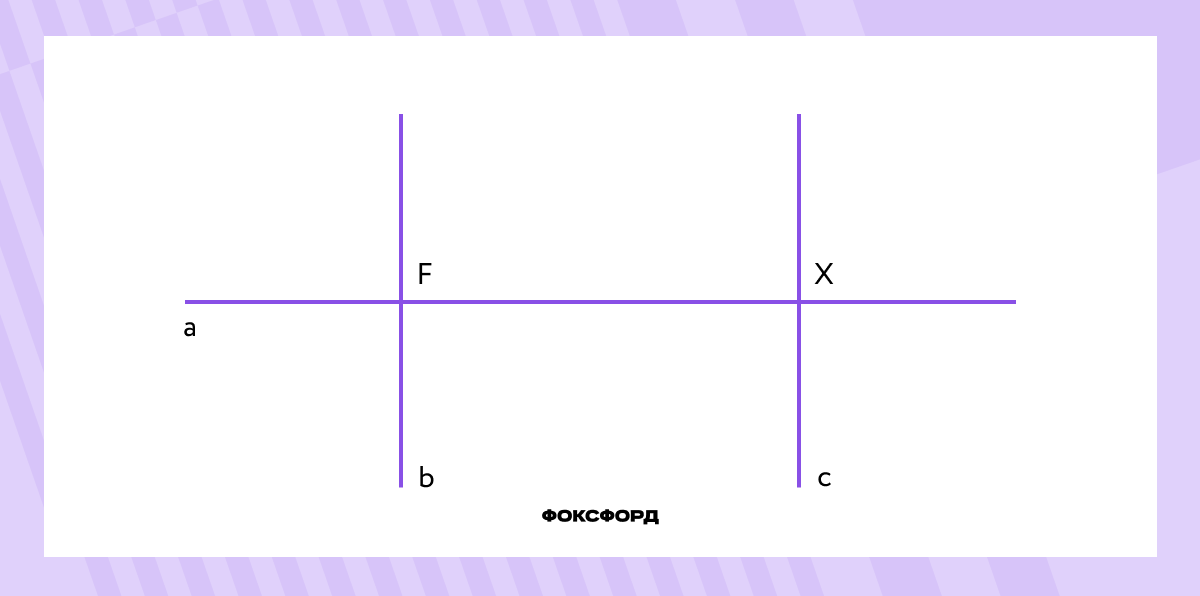
Пусть a⟂b и a⟂c. Прямые b и сне пересекаются, ведь если бы существовала точка их пересечения, значит, через неё проходили бы две прямые, перпендикулярные a, что невозможно согласно теореме о перпендикулярных прямых. Следовательно, b||с.
Использование знания о перпендикулярных прямых
- Математика и геометрия. Знание о перпендикулярности помогает решать множество задач. Например, построение высоты треугольника.
- Строительство и архитектура. Без соблюдения перпендикулярности невозможно спроектировать устойчивые конструкции.
- Чертёж и техническая графика. Перпендикулярные линии применяются для построения оси координат, разметки деталей, границ объектов.
- Картография и навигация. В морской и авиационной навигации понятие перпендикулярного курса важно для точных поворотов и расчётов маршрута.
- Программирование и компьютерная графика. Расчёты тени, света и отражений в 3D-графике используют векторы, которые могут быть перпендикулярными.
- Повседневные задачи. Например, развешивание полок или укладка плитки.
Ответим на ваши вопросы
Свяжемся с вами в течение 5 минут и проведём бесплатную консультацию по вопросам перехода на домашнее обучение
Позвоним с 8 до 21 в рабочие дни






