Разбираемся в решении линейных уравнений

Системой линейных алгебраических уравнений (СЛАУ) называется объединение n линейных уравнений, каждое из которых содержит k переменных. Вот несколько методов решения систем линейных уравнений.

Решение системы линейных уравнений методом подстановки («школьный метод»)

Это самый лёгкий способ решения систем линейных уравнений. Его алгоритм достаточно прост и заключается в следующем:

1. Одна переменная из одного линейного уравнения выражается через другую переменную.
2. Выраженная переменная подставляется в другое уравнение системы.
3. Полученное уравнение, содержащее только одну переменную, решается относительно этой переменной.
4. Значение переменной, полученное в пункте 3, подставляется в выражение для другой (первой) переменной (см. пункт 1).

Подписывайтесь на телеграм-канал Домашней школы Фоксфорда — здесь мы каждый день публикуем полезные посты о лайфхаках обучения, тайм-менеджменте, развитии и поддержке школьников, а ещё делимся бесплатными материалами и шпаргалками.

Рассмотрим пример.

Согласно первому пункту алгоритма решения СЛАУ, нужно выразить одну переменную через другую. В данном случае удобно из второго уравнения системы выразить переменную y через переменную x. Далее подставим переменную y, выраженную через x, в первое уравнение системы. Получим новое выражение.

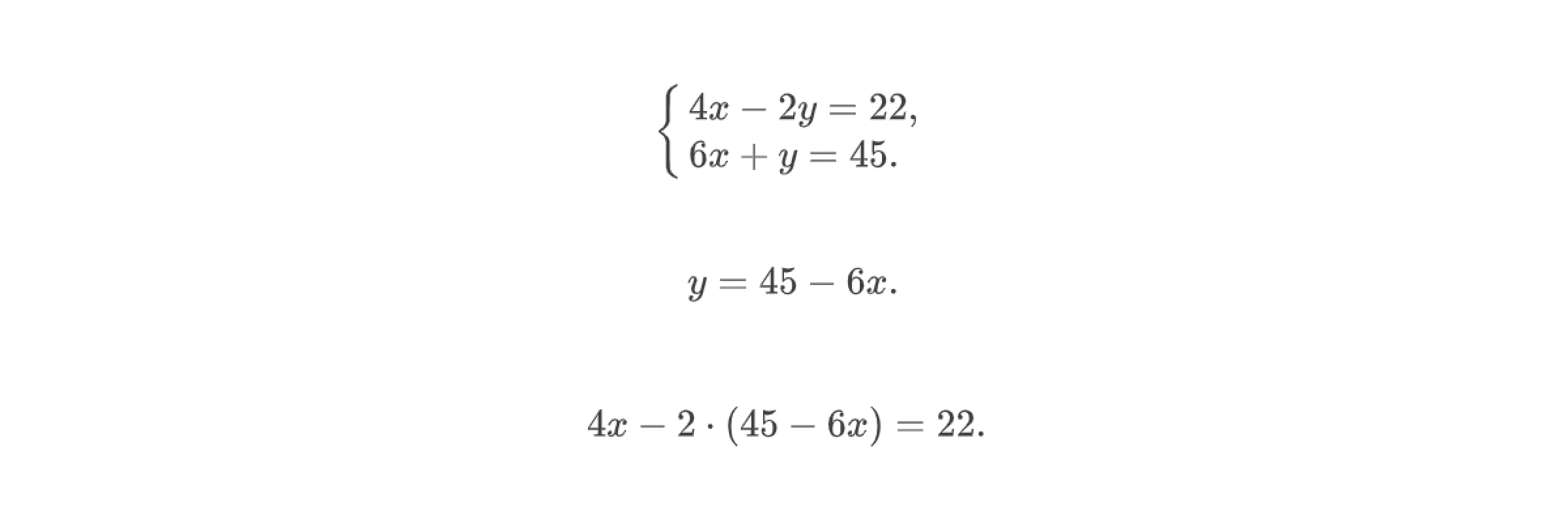
Тогда можно записать систему уравнений, равносильную первой. Раскроем скобки и приведём первое уравнение системы к виду 16x = 112, откуда x = 7.

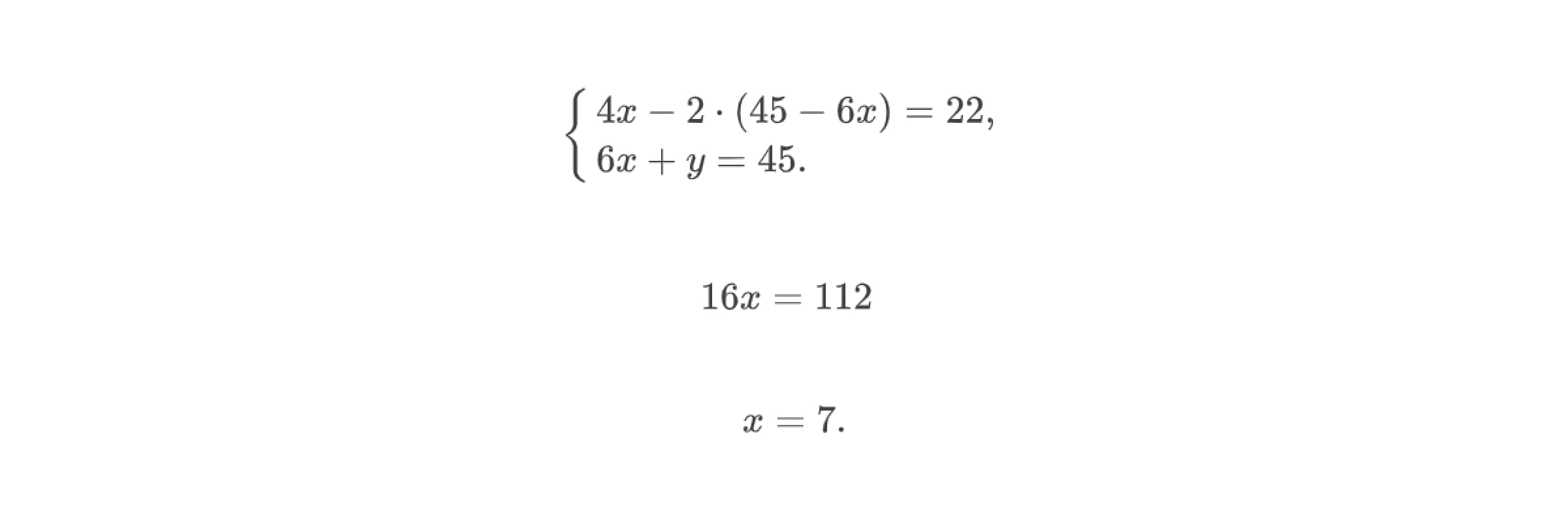
Теперь найдём значение y, подставив значение переменной x в выражение для второй переменной.

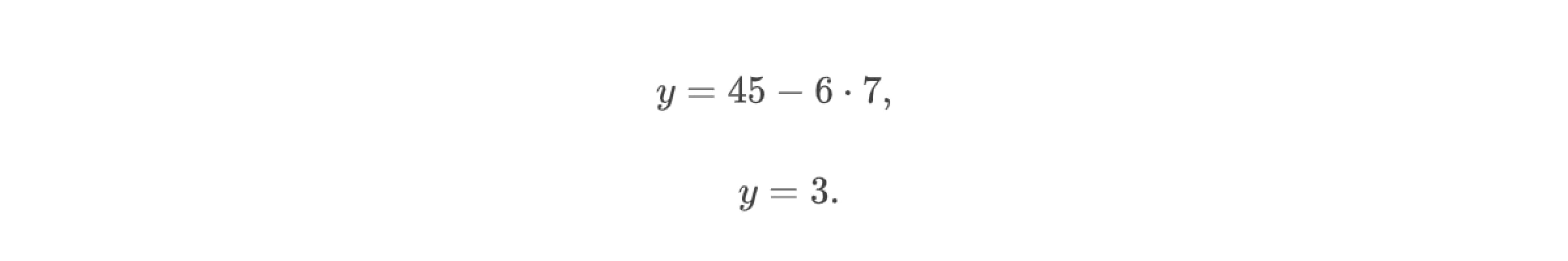
Применив метод подстановки к рассматриваемой системе линейных уравнений, мы нашли пару чисел (7; 3) — её решение.

<<Форма демодоступа>>

Решение системы линейных уравнений методом почленного сложения (вычитания) уравнений системы

Суть метода состоит в избавлении от одной из переменных в системе уравнений, алгоритм метода достаточно простой:

1. Все уравнения системы почленно умножаются на такое число, чтобы коэффициенты при одной из переменных стали противоположными числами (если коэффициенты при одной из переменных уже являются противоположными числами, то можно сразу переходить к пункту 2).
2. Правая и левая части каждого уравнения почленно складываются, получается уравнение с одной переменной.
3. Полученное уравнение решается относительно единственной переменной.
4. Значение найденной переменной подставляется в одно из исходных уравнений системы, далее определяется значение второй переменной.

В качестве примера решим систему уравнений. Здесь будет достаточно просто «избавиться» от переменной y. Для этого почленно умножим обе части первого уравнения системы на 2 и получим равносильную систему уравнений.

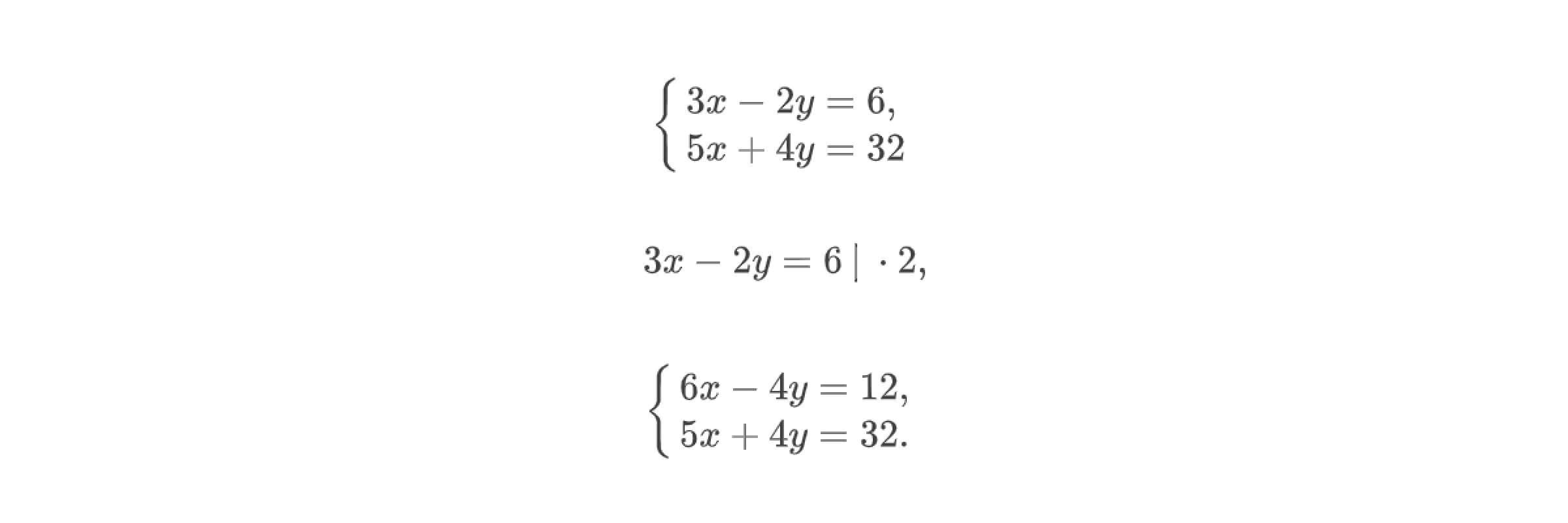
Теперь прибавим к левой части первого уравнения левую часть второго уравнения, а к правой части первого уравнения — правую часть второго. В итоге получим уравнение вида 11x = 44. Решим это уравнение относительно единственной переменной: x = 4. Подставим найденное значение в первое уравнение исходной системы и найдём значение y.

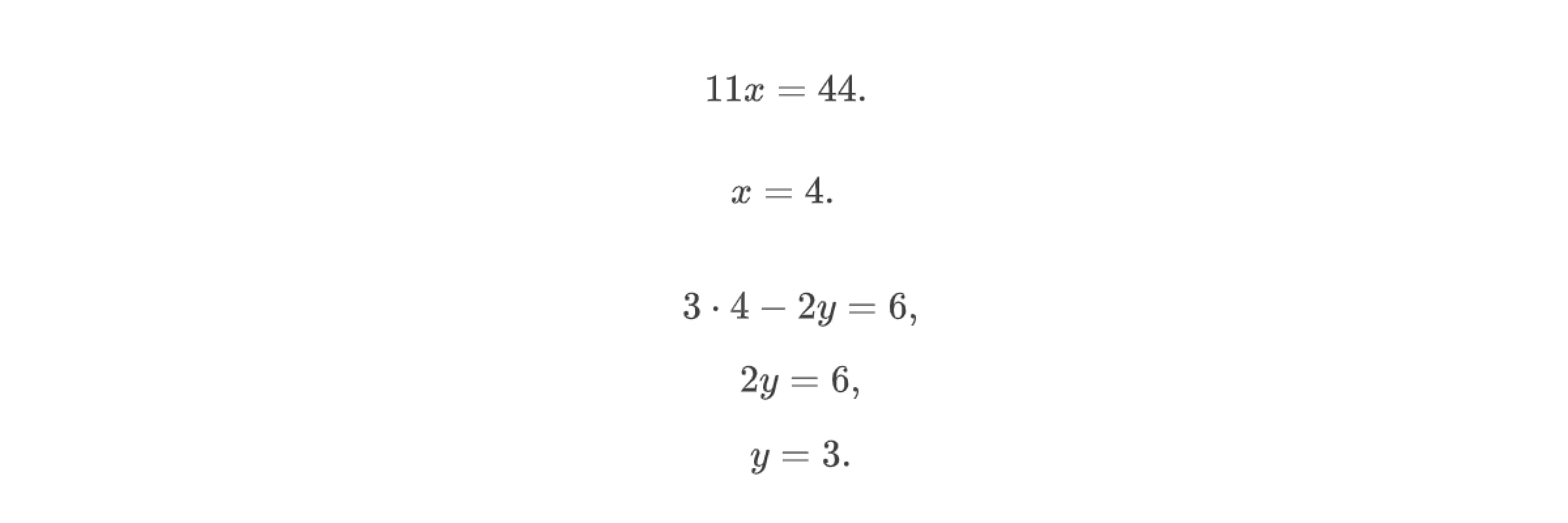
Итак, пара чисел (4; 3) — решение системы линейных уравнений с двумя переменными. Решение мы получили методом сложения.

Решение системы линейных уравнений по формулам Крамера

Чтобы решить систему линейных уравнений методом Крамера, нужно познакомиться с понятием определителя.

Определение

Определителем системы называют запись чисел в квадратной таблице, в соответствие которой ставится число по некоторому правилу.

Правило таково: пусть даны четыре числа a, b, c, d. Пусть они имеют следующее расположение в квадратной таблице:

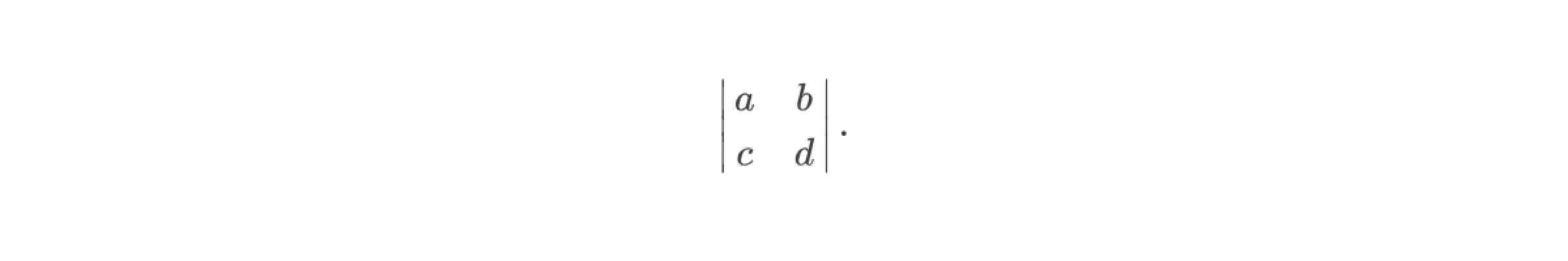
Значение определителя системы в этом случае находится по формуле:

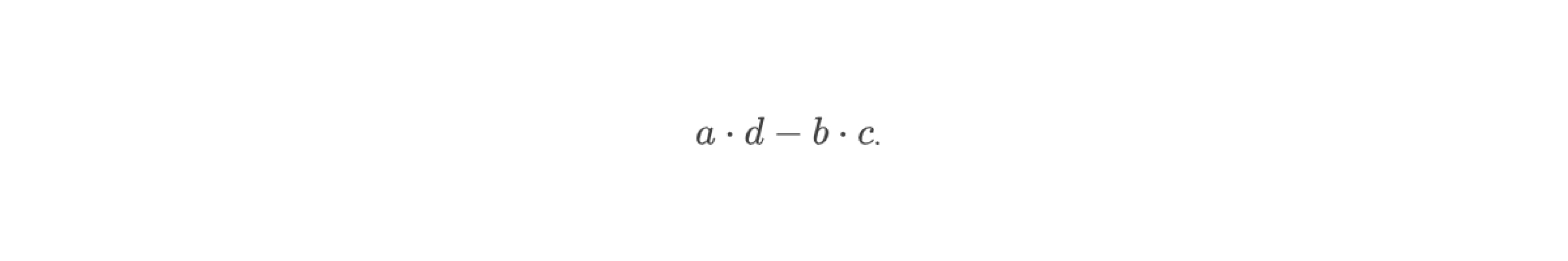
Определитель, составленный из коэффициентов при переменных в линейной системе уравнений, называется главным определителем системы. Будем обозначать его Δ. Например, у рассмотренной выше системы уравнений

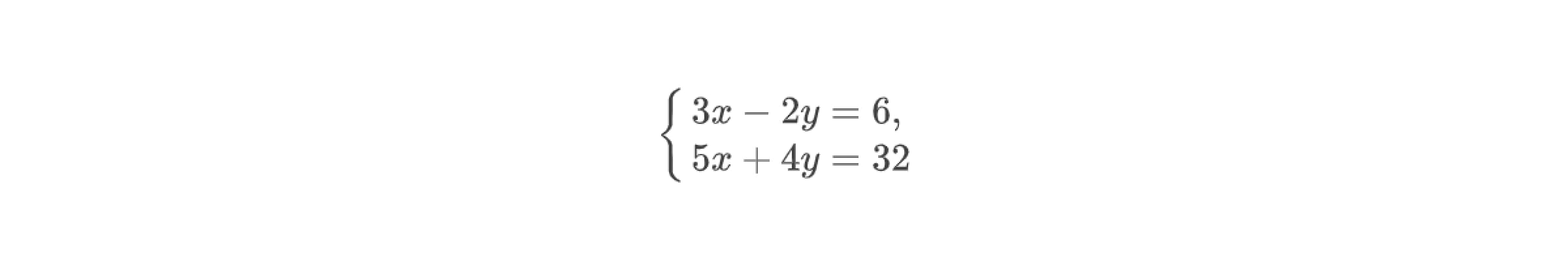
главный определитель будет иметь вид:

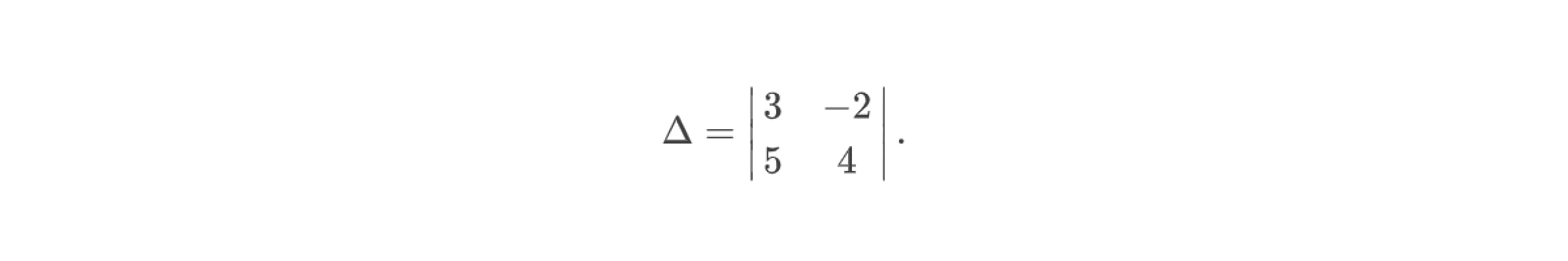
Найдём его значение:

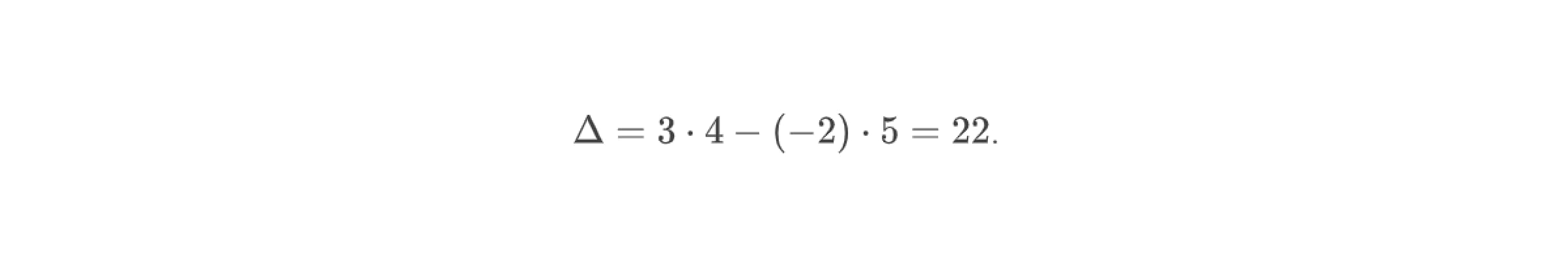
Для решения системы линейных уравнений методом Крамера нам понадобятся ещё два определителя, которые называются вспомогательными:

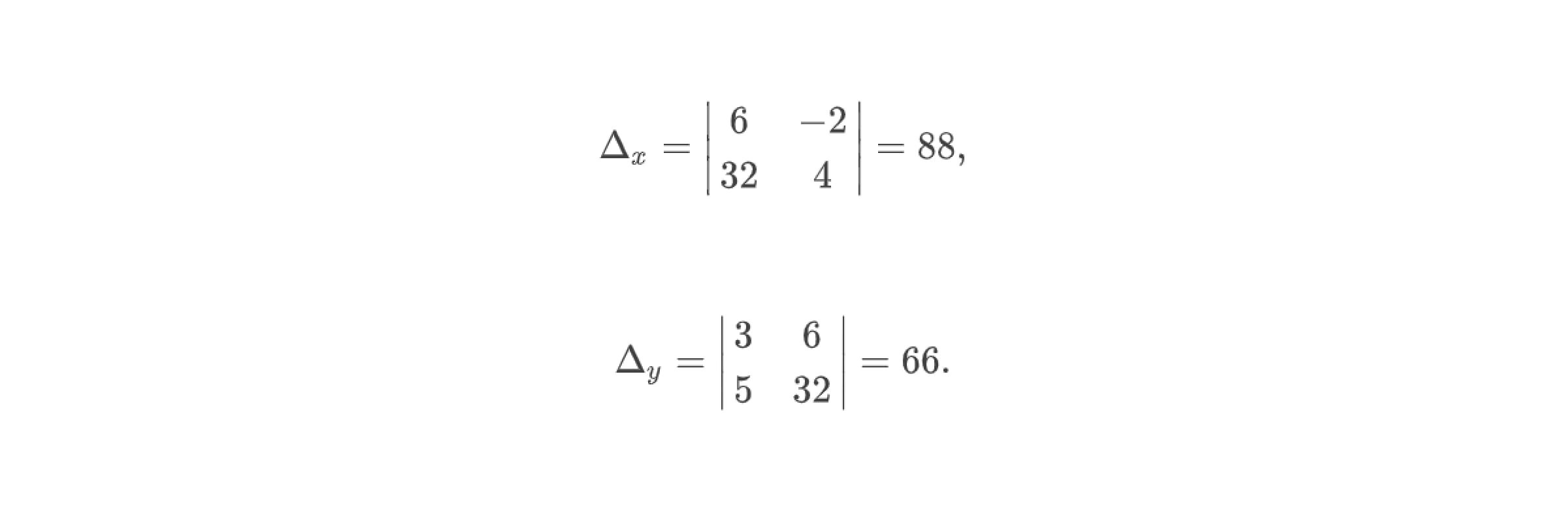
Отметим, что в данные определители уже входят правые части каждого уравнения системы. Так, в определитель Δₓ первым столбцом записываем правые части уравнений (так называемые свободные члены уравнений), второй столбец оставляем таким же, как в главном определителе системы. В определитель Δ_у вторым столбцом записываем правые части уравнений, а первый столбец оставляем таким же, как в главном определителе системы.

Итак, формулы Крамера для решения системы двух линейных уравнений с двумя переменными: 

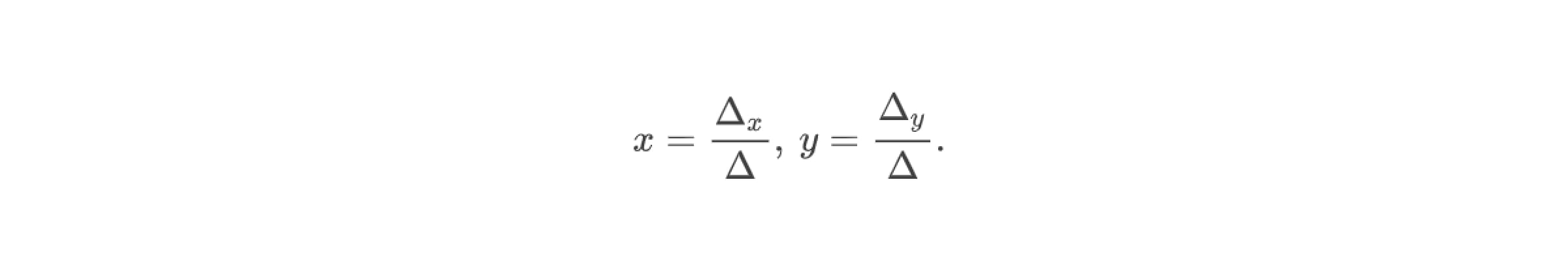
Отметим, что данный метод решения СЛАУ можно применять лишь в тех случаях, когда Δ ≠ 0.

Убедимся в том, что данные формулы работают, подставив в них ранее найденные значения определителей.

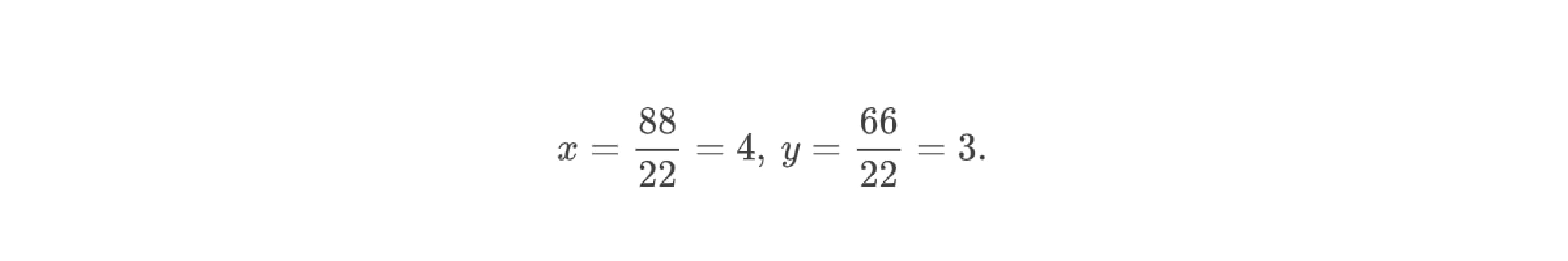
Пара чисел (4; 3) действительно является решением данной системы уравнений.

Обобщим алгоритм нахождения решений системы двух линейных уравнений с двумя переменными методом Крамера. Пусть дана система линейных уравнений: 

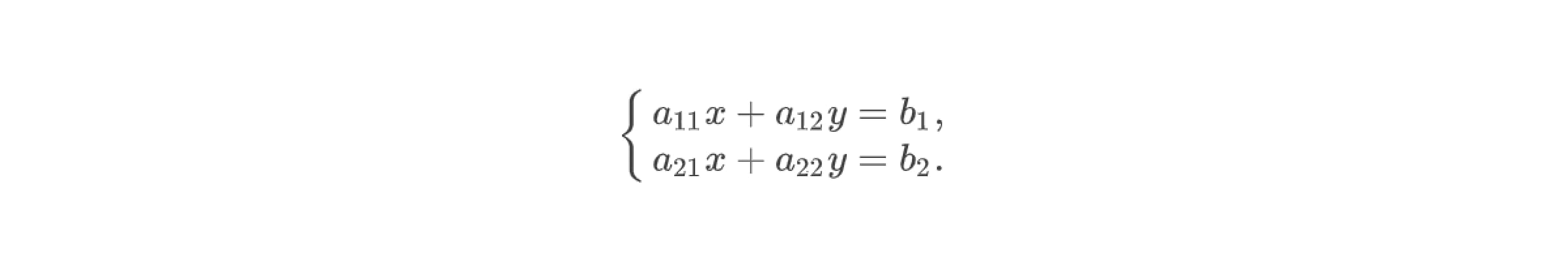
Нужно: 

1. Вычислить главный определитель системы.

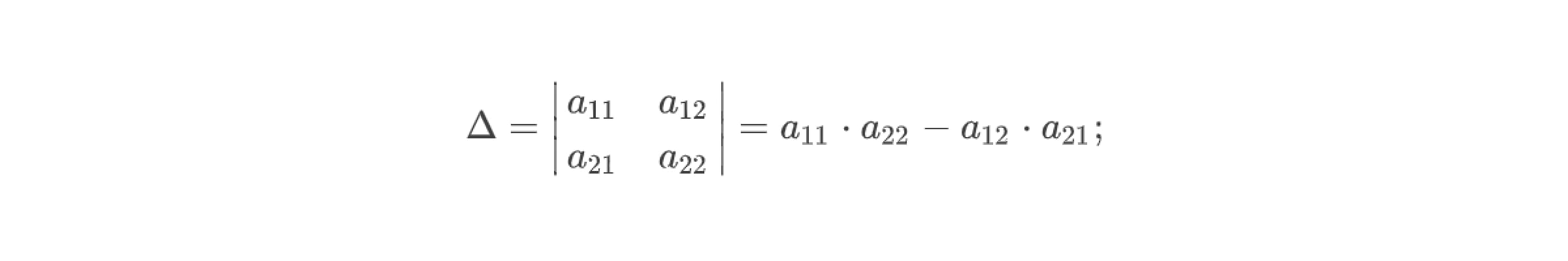
2. Вычислить вспомогательные определители.

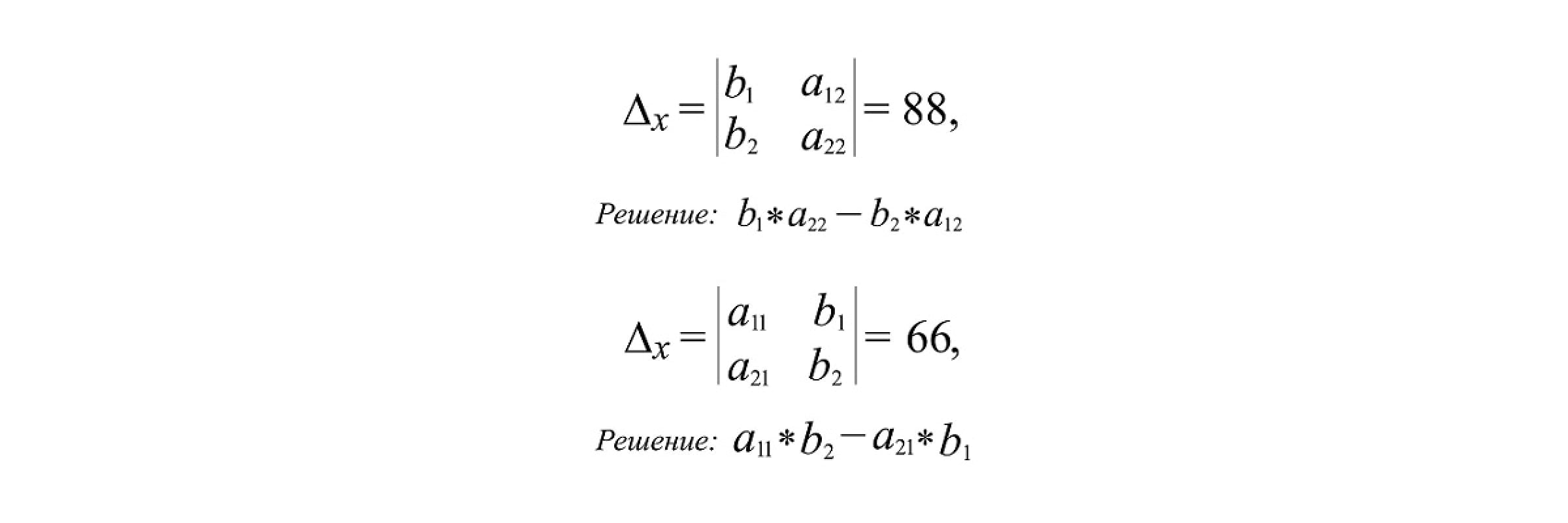
3. Применить формулы Крамера и найти решение системы.

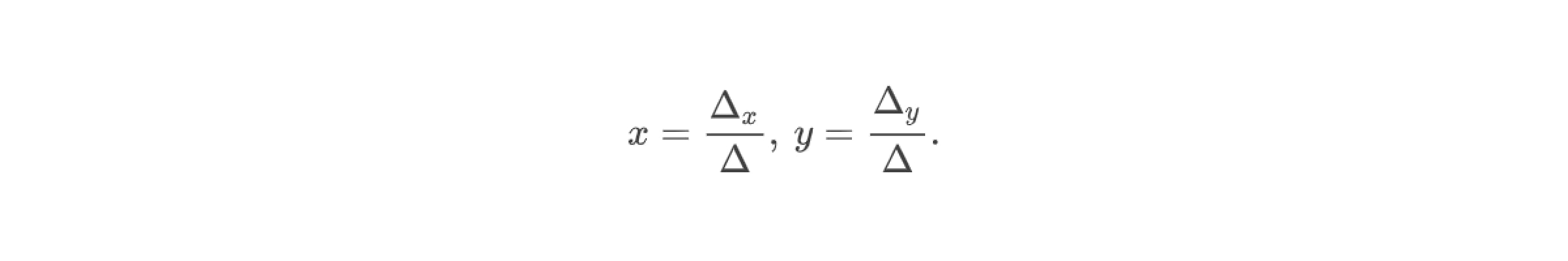
Решение системы линейных уравнений с помощью обратной матрицы

Матрицей системы линейных уравнений называется таблица, составленная из коэффициентов при переменных. Так, для системы вида 

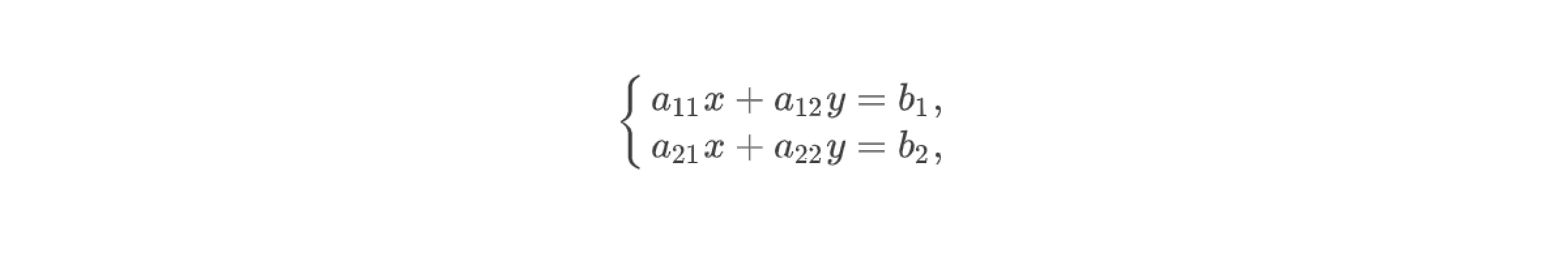
матрицей A является

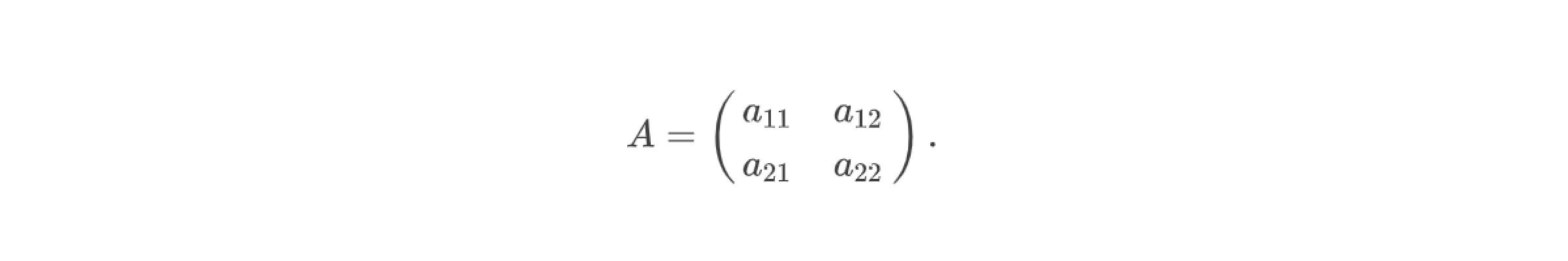
Столбцом свободных коэффициентов будем называть

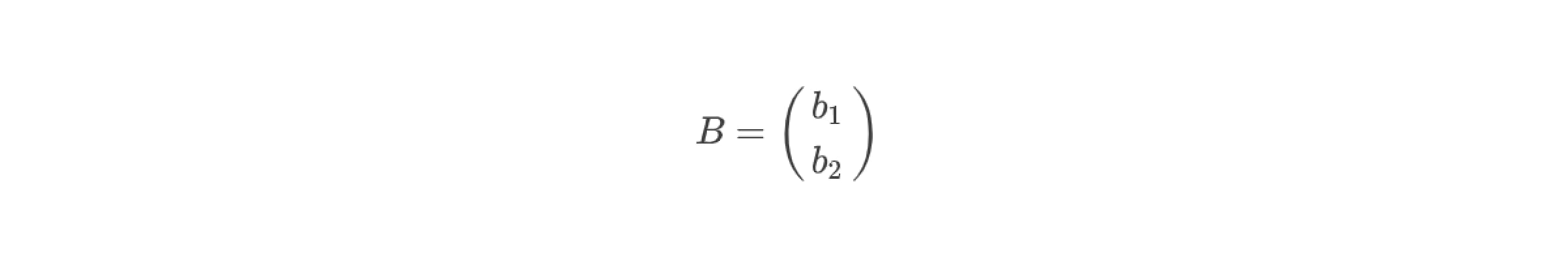
а столбцом переменных —

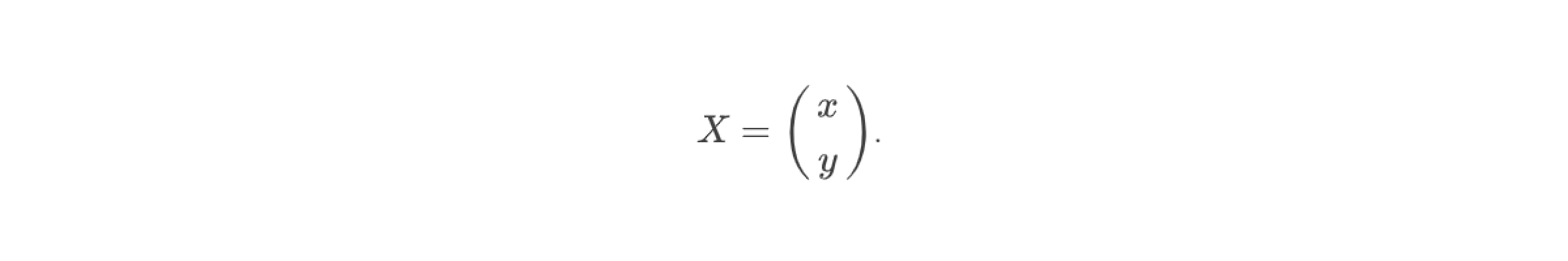
Тогда систему уравнений можно переписать в виде

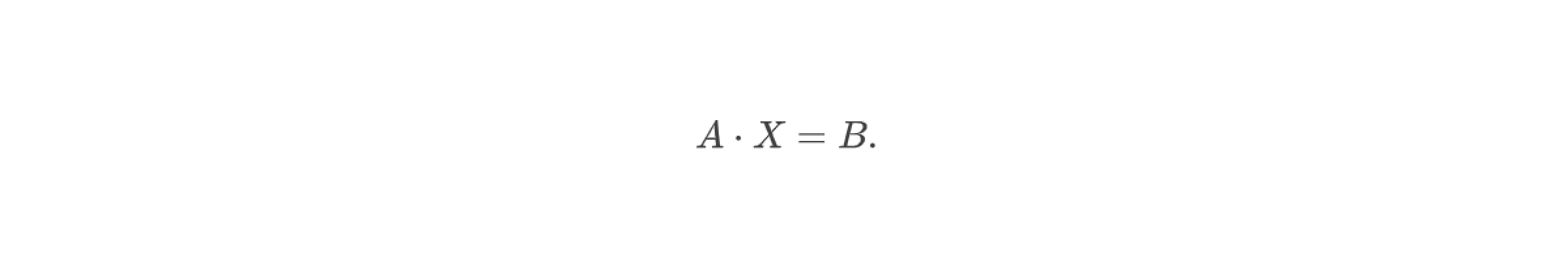
Поясним, как происходит умножение матрицы на столбец. В матрице A есть строки: (а₁₁, а₁₂) и (а₂₁, а₂₂) а также столбцы (а₁₁, а₂₁) и (а₁₂, а₂₂).

При умножении матрицы на столбец X получается столбец, а само умножение происходит по следующему правилу:

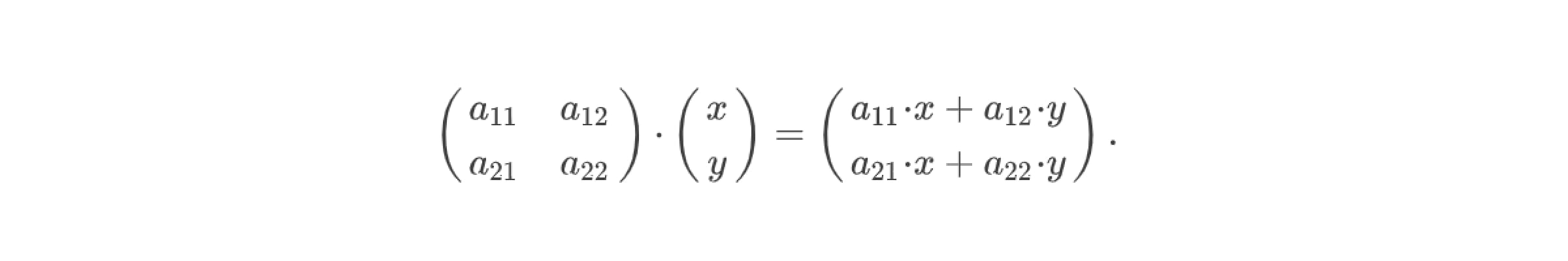
Для нахождения обратной матрицы, которая обозначается как А⁻¹ , нам потребуется умение находить определитель матрицы, что подробно описано в пункте о решении системы линейных уравнений по формулам Крамера, и умение находить транспонированную матрицу T. Для того чтобы записать матрицу, транспонированную к данной, нужно лишь поменять столбцы и строки местами. Например, для матрицы A транспонированной будет матрица: 

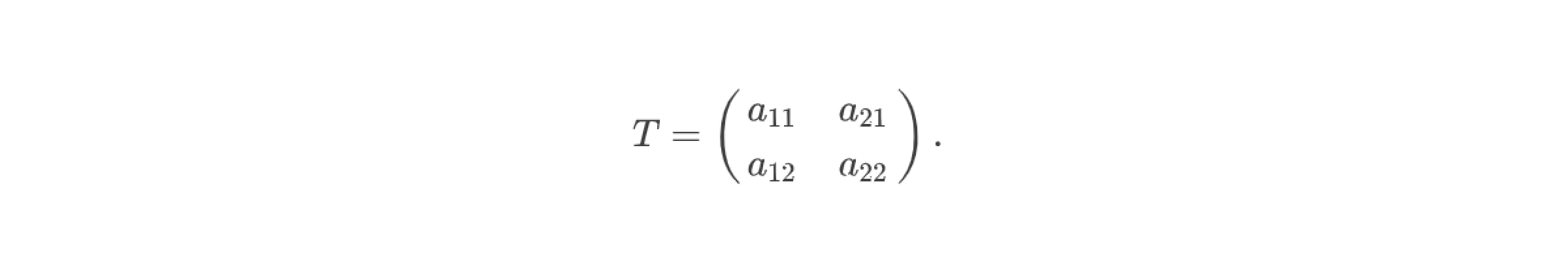
Рассмотрим алгоритм поиска обратной матрицы.

1. Вычислить определитель матрицы A.

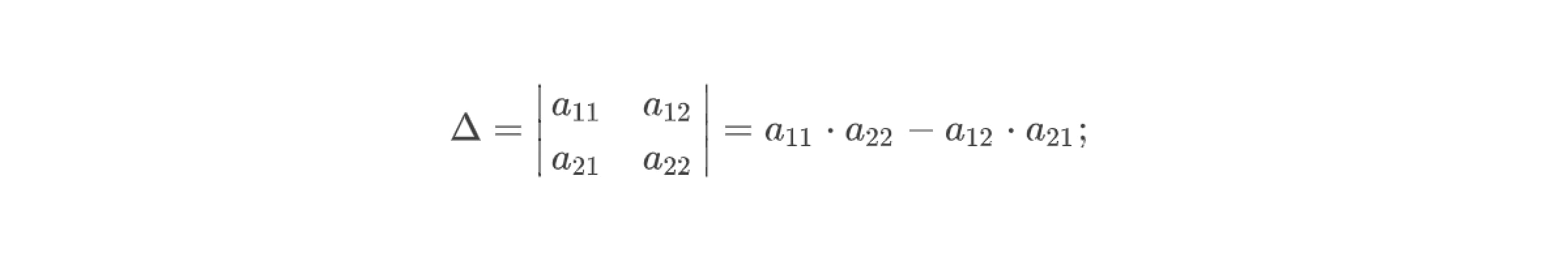
2. Записать матрицу миноров M. Для этого нужно просто переставить числа в матрице A следующим образом:

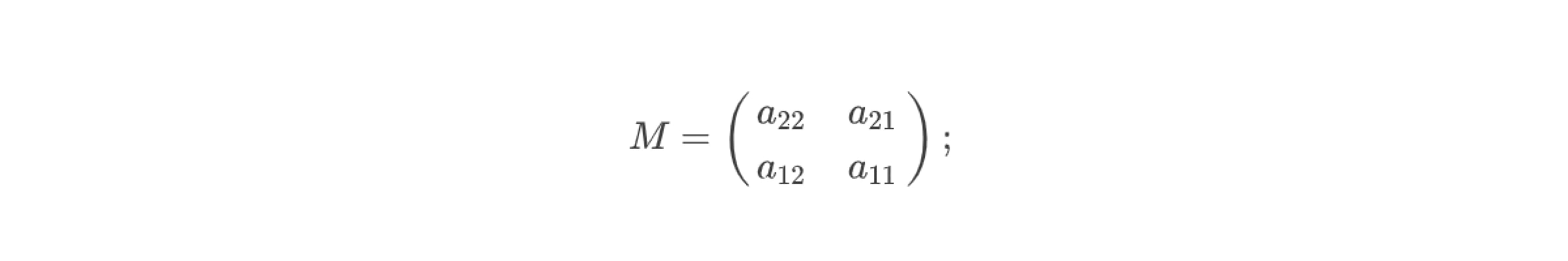
3. Записать матрицу алгебраических дополнений А  ͙ — для этого необходимо лишь поменять знаки коэффициентов а₁₂ и а₂₁ в матрице миноров M, в результате чего получим

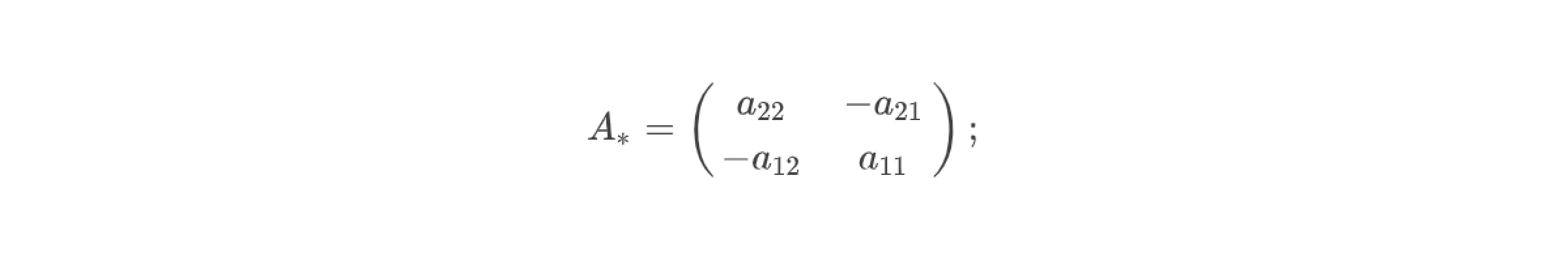
4. Записать матрицу, транспонированную к матрице алгебраических дополнений:

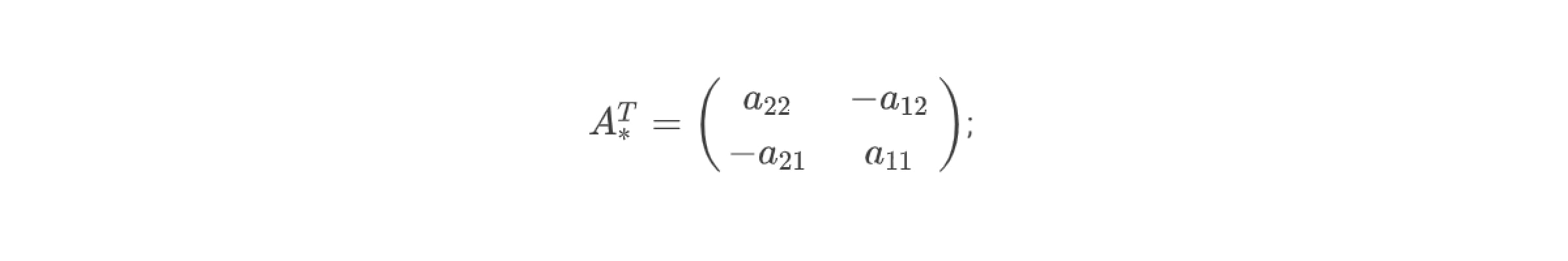
5. Найти обратную матрицу А⁻¹, разделив каждый элемент матрицы Аᵀ ͙ на значение определителя матрицы A, то есть

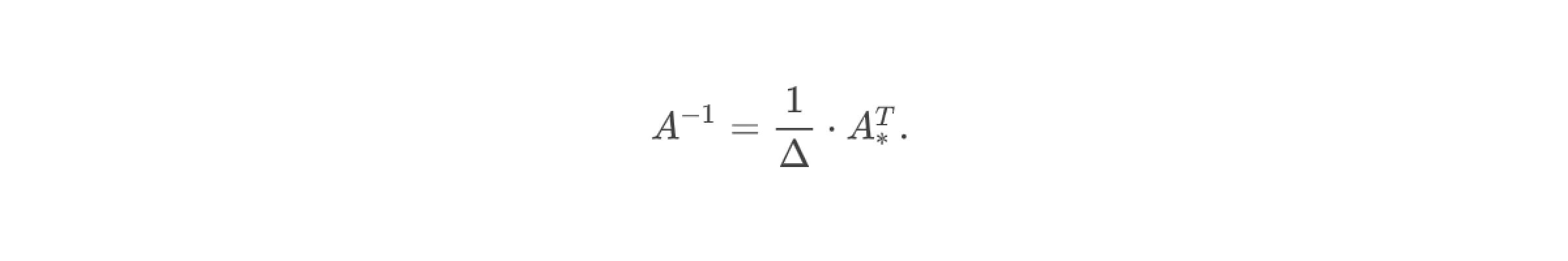
6. Для нахождения неизвестных нужно полученную обратную матрицу А⁻¹ умножить на столбец свободных коэффициентов:

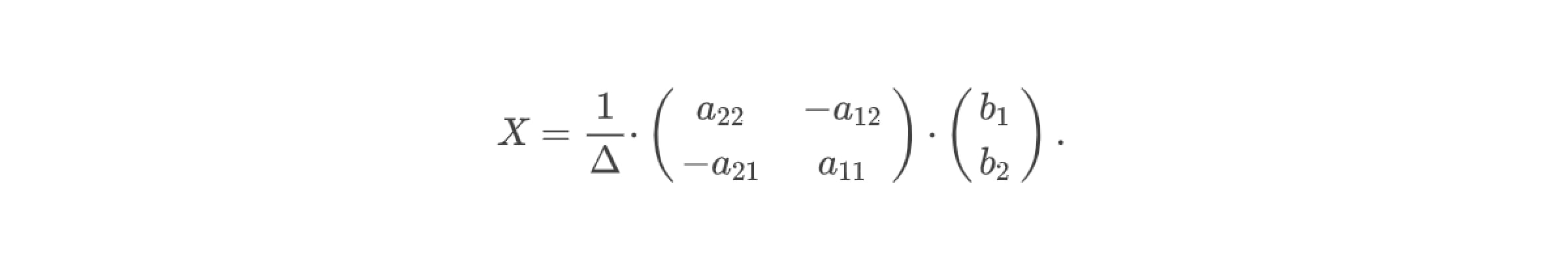
Поясним всё на примере решения системы линейных уравнений с двумя переменными:

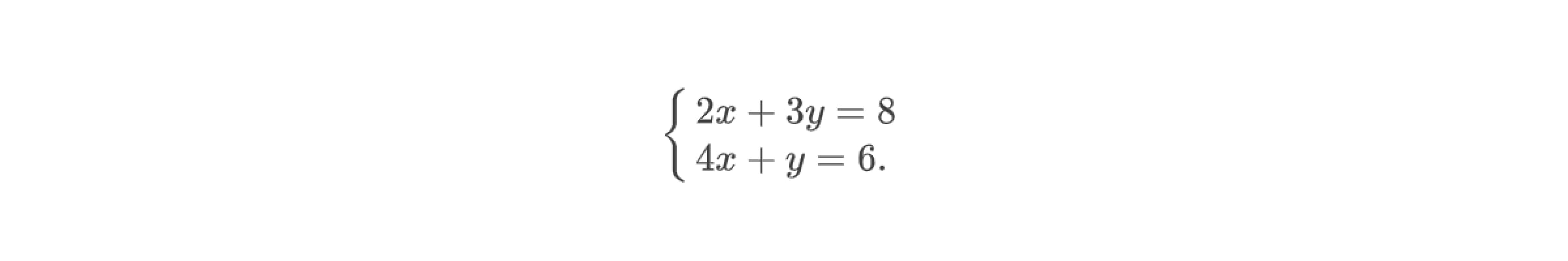
Матрица системы:

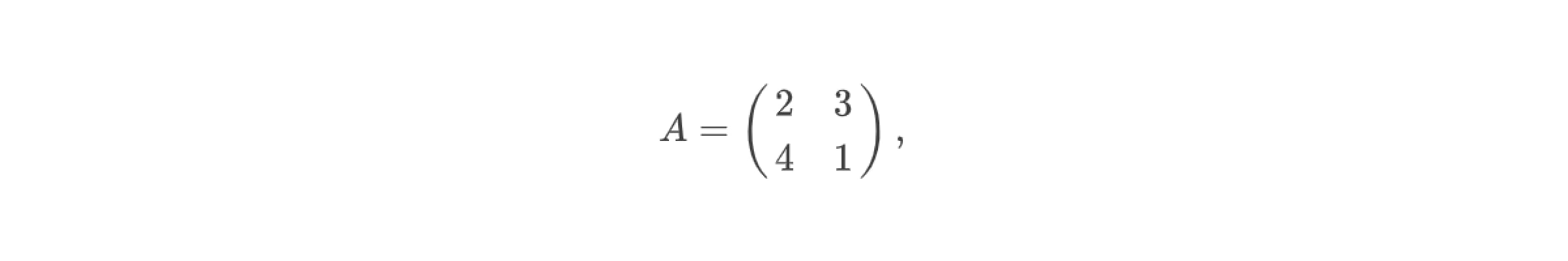
Столбец свободных коэффициентов:

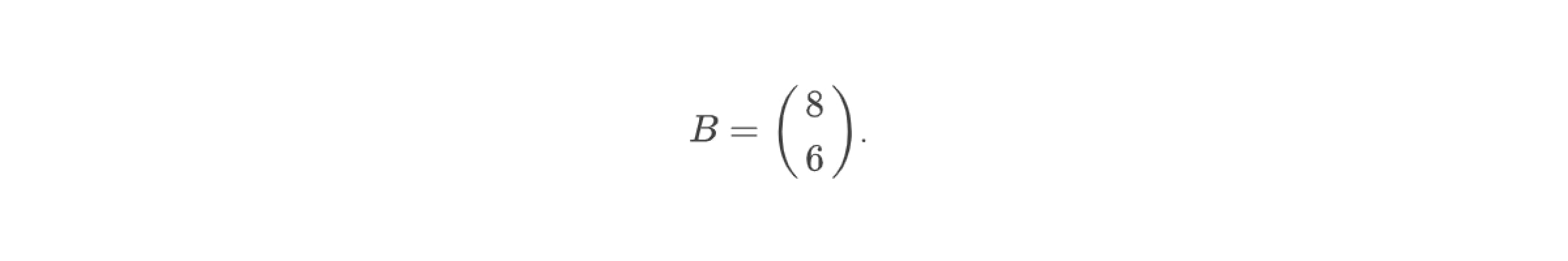
Следуя алгоритму решения СЛАУ, найдём обратную матрицу.

1. Определитель матрицы A равен

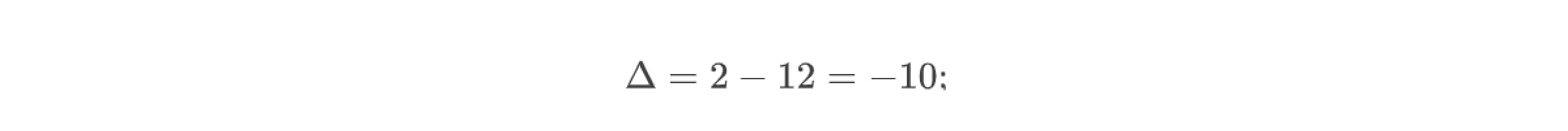
2. Матрица миноров:

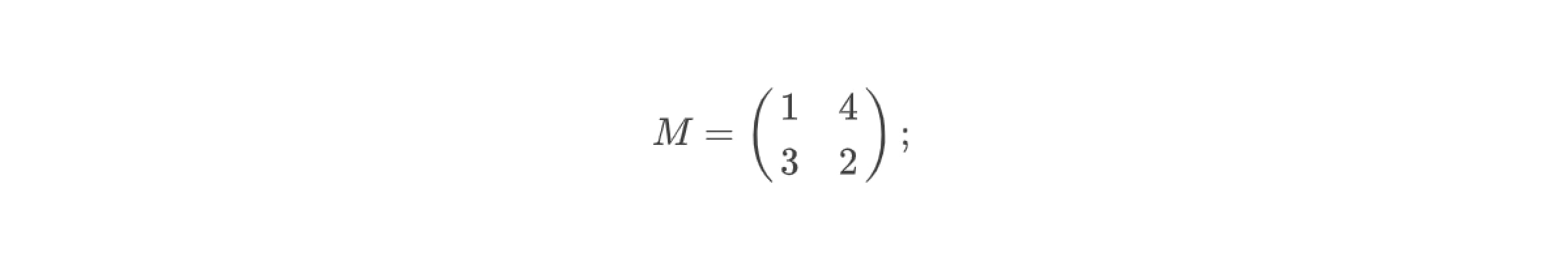
3. Матрица алгебраических дополнений:

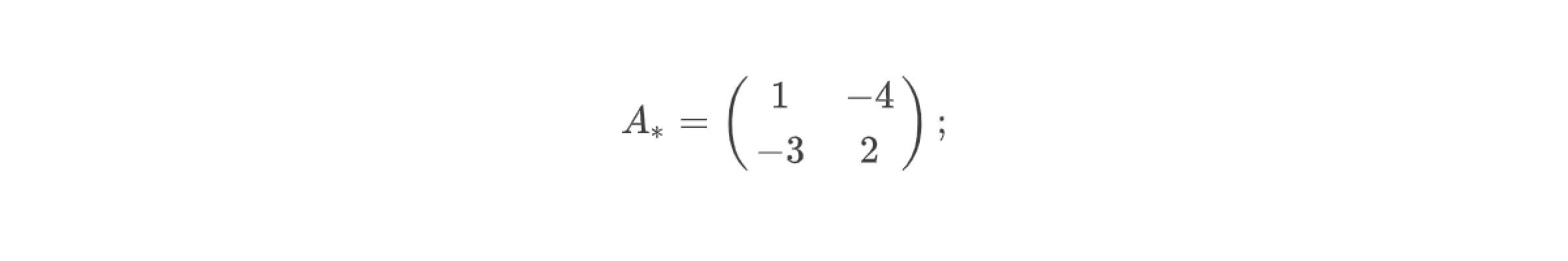
4. Матрица, транспонированная к матрице алгебраических дополнений:

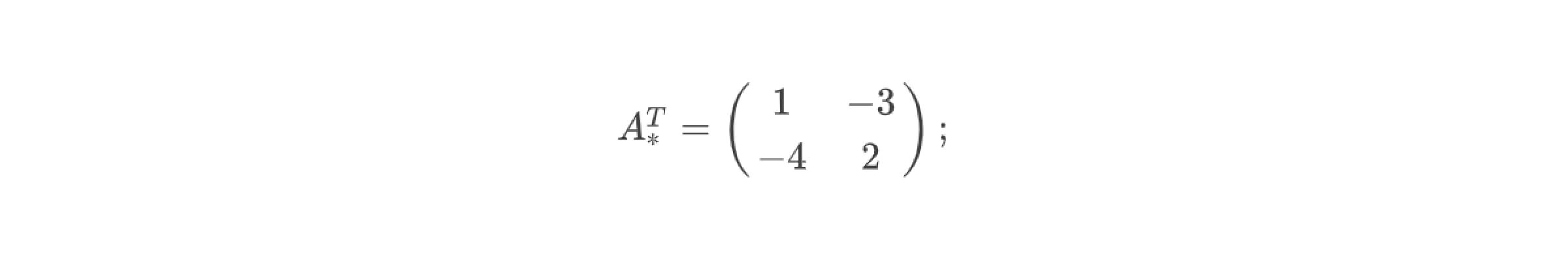
5. Обратная матрица:

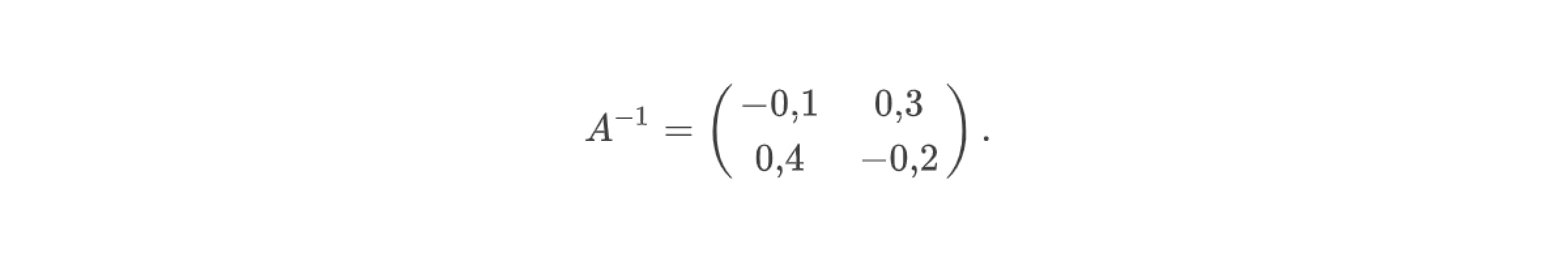
Теперь умножим найденную обратную матрицу на столбец свободных коэффициентов:

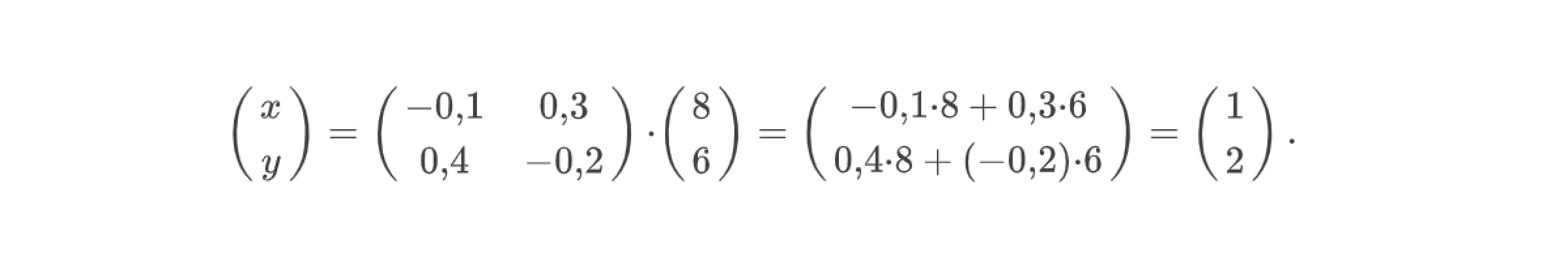
Пара чисел (1; 2) — решение данной системы уравнений.

Решение системы линейных уравнений методом Гаусса

Этот метод позволяет достаточно легко находить решения систем линейных уравнений, в которых более двух уравнений и неизвестных. По сути, этот метод — обобщение метода подстановки. Рассмотрим этот способ на примере системы трёх уравнений с тремя неизвестными. 

На первом этапе решения систему уравнений необходимо привести к трапециевидной форме, которая выглядит следующим образом:

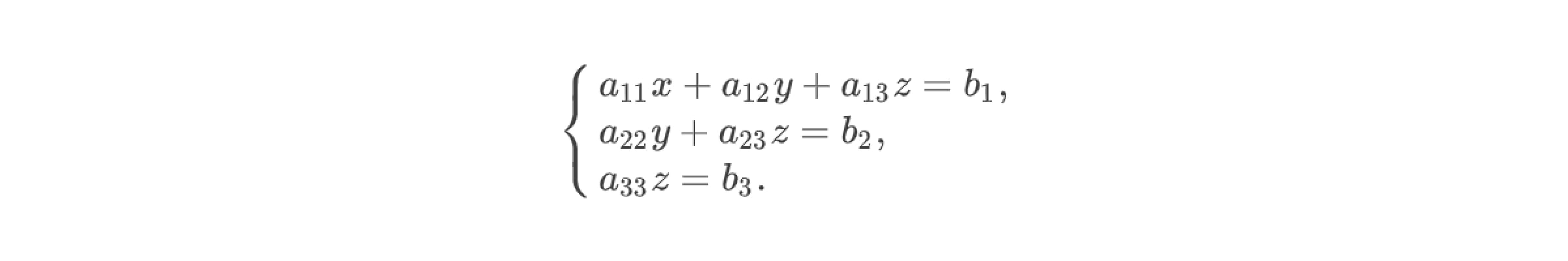
Для этого нужно провести несложные линейные преобразования с коэффициентами расширенной матрицы системы. Расширенная матрица системы отличается от матрицы системы лишь тем, что она содержит ещё и столбец правых частей уравнений, который записывается справа. Преобразования включают в себя сложение или вычитание строк матрицы, а также умножение элементов строки на число.

Применим данный метод к системе линейных уравнений с тремя переменными:

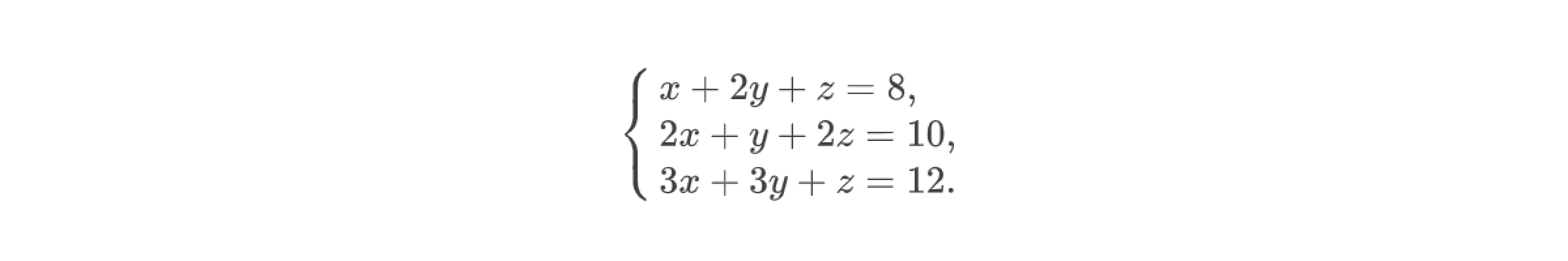
Расширенная матрица A данной системы принимает вид:

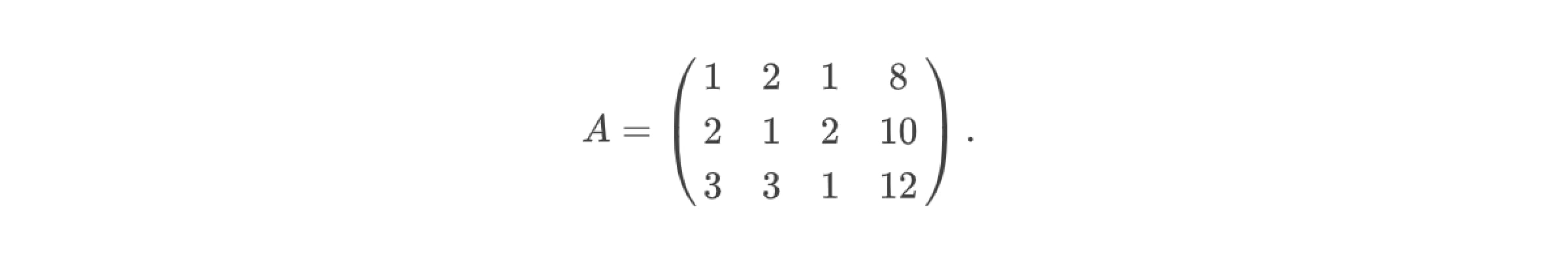
Проводя преобразования строк, нужно добиться того, чтобы в третьей строке расширенной матрицы на первом и втором местах были нули, а во второй строке — нуль на первом месте (возможно, при этом во второй строке будет ещё нуль и на третьем месте).

Вначале вычтем из второй строки матрицы первую строку, умноженную на два, в результате во второй строке окажется два нуля. Затем вычтем из третьей строки первую строку, умноженную на три, в результате чего в третьей строке окажется только один ноль:

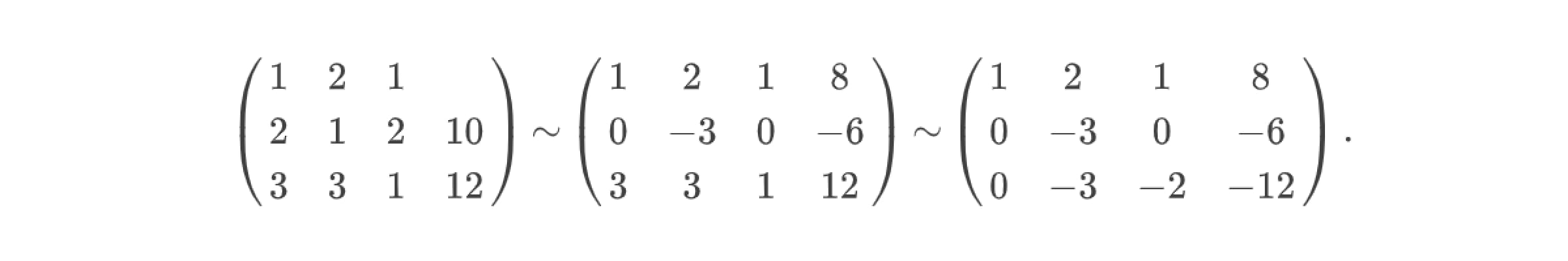
С одной стороны, можно остановиться на данном этапе, поменять вторую и третью строку местами, решить систему уравнений, соответствующую полученной расширенной матрице: 

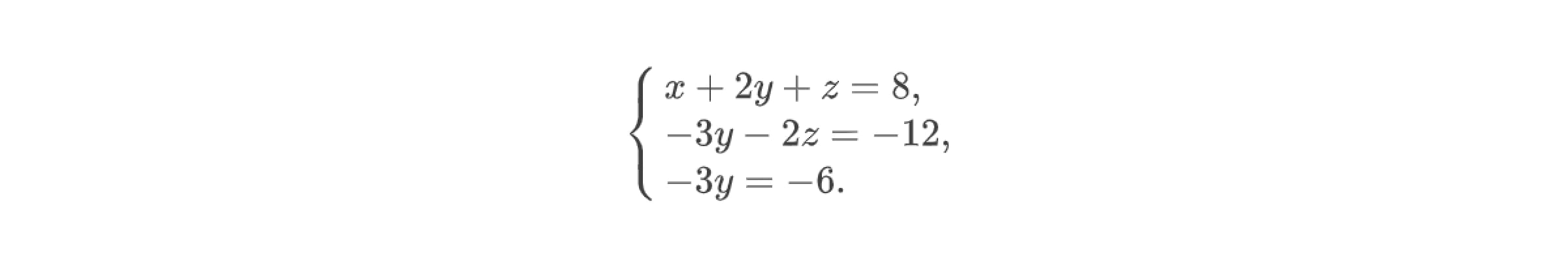
С другой стороны, следуя алгоритму решения системы уравнений, необходимо вычесть из третьей строки расширенной матрицы вторую строку и получить два нуля в последней строке матрицы:

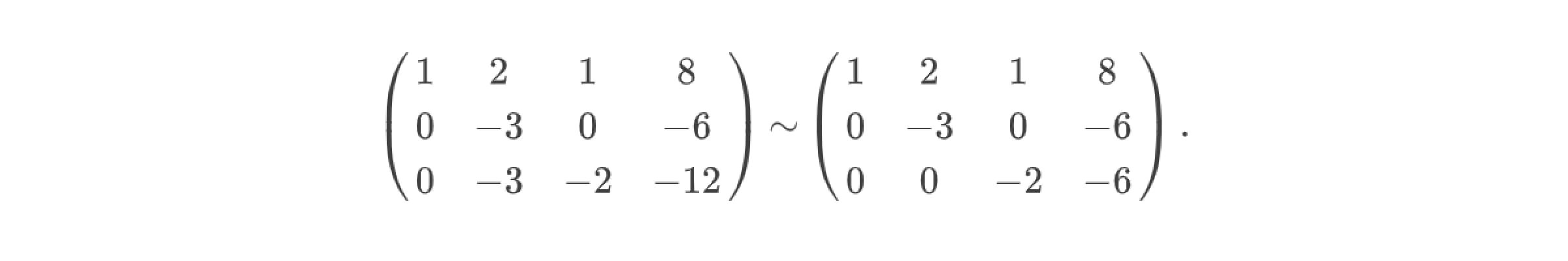
Это позволит перейти к решению ещё более простой системы линейных уравнений:

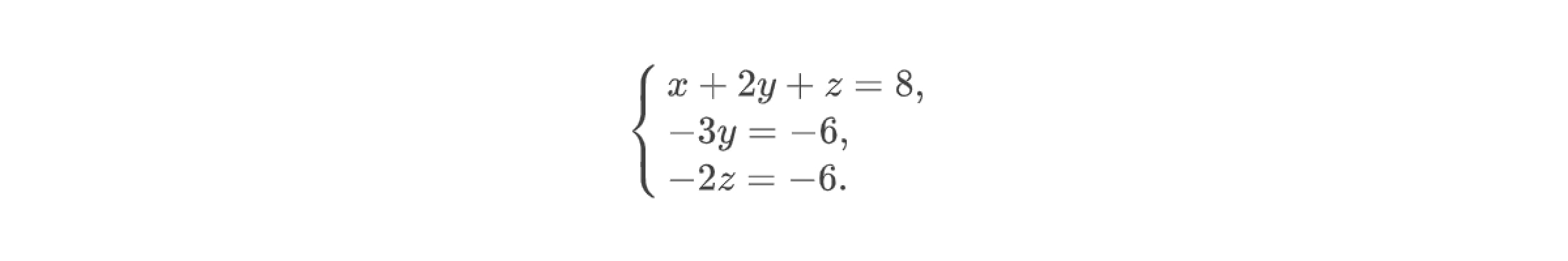
Теперь реализуем обратный ход метода Гаусса: из третьего уравнения системы определим z = 3 , из второго — y = 2. Далее используем метод подстановки и определим значение x:

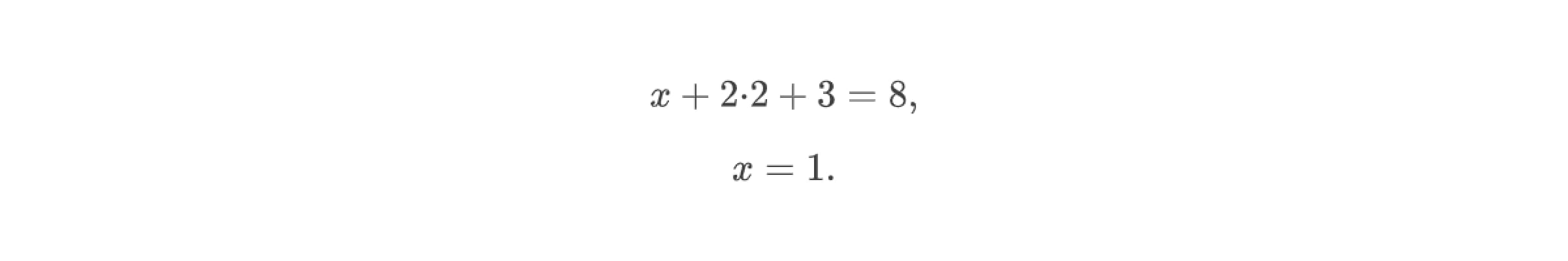
Итак, решение системы линейных уравнений методом Гаусса: x = 1, y = 2, z = 3.

Заключение

В этой статье мы разобрали следующие основные способы решения систем линейных уравнений:

• метод подстановки, или «школьный метод», 
• метод почленного сложения или вычитания, 
• метод Крамера, 
• решение с помощью обратной матрицы, 
• метод Гаусса.