
Что такое функция
До того как начинать работу с графиками, важно понять, что такое функция и зачем она нужна.
Функция — это математическое правило. Оно устанавливает, как одна переменная величина (x) влияет на другую (y).
Правило обычно описывается формулой — набором математических действий, которые выполняют над независимой переменной x. В результате получается значение, или зависимая переменная y.
Например, y = x + 1 устанавливает, что y будет на единицу больше, чем любое число, которое мы можем подставить вместо переменной x.
Правило может и не быть формулой, к примеру, оно может быть просто описано словами. Сам по себе график тоже может задавать функцию — тогда каждому значению x соответствует y точки на графике.
Функция — это ещё и соответствие двух множеств друг другу.
Одно из них — это множество возможных значений для x, а другое — множество возможных значений для y. При этом каждому значению x соответствует одно и только одно определённое значение y. Оно получается после вычислений по формуле.
В каждом из множеств может быть очень много значений. Чтобы проанализировать функцию, не нужно вычислять их все. Вместо этого можно построить график.
Что такое график функции
График — наглядное представление функции.
Он выглядит как линия или группа линий на координатной плоскости с осями Ox и Oy. Его проводят через множество точек, координатам каждой из которых соответствуют определённые значения x и y. Находить вообще все x и y необязательно. Чтобы построить линию, достаточно определить ключевые точки, через которые она должна пройти. Для этого функцию исследуют — то есть выявляют её главные свойства.
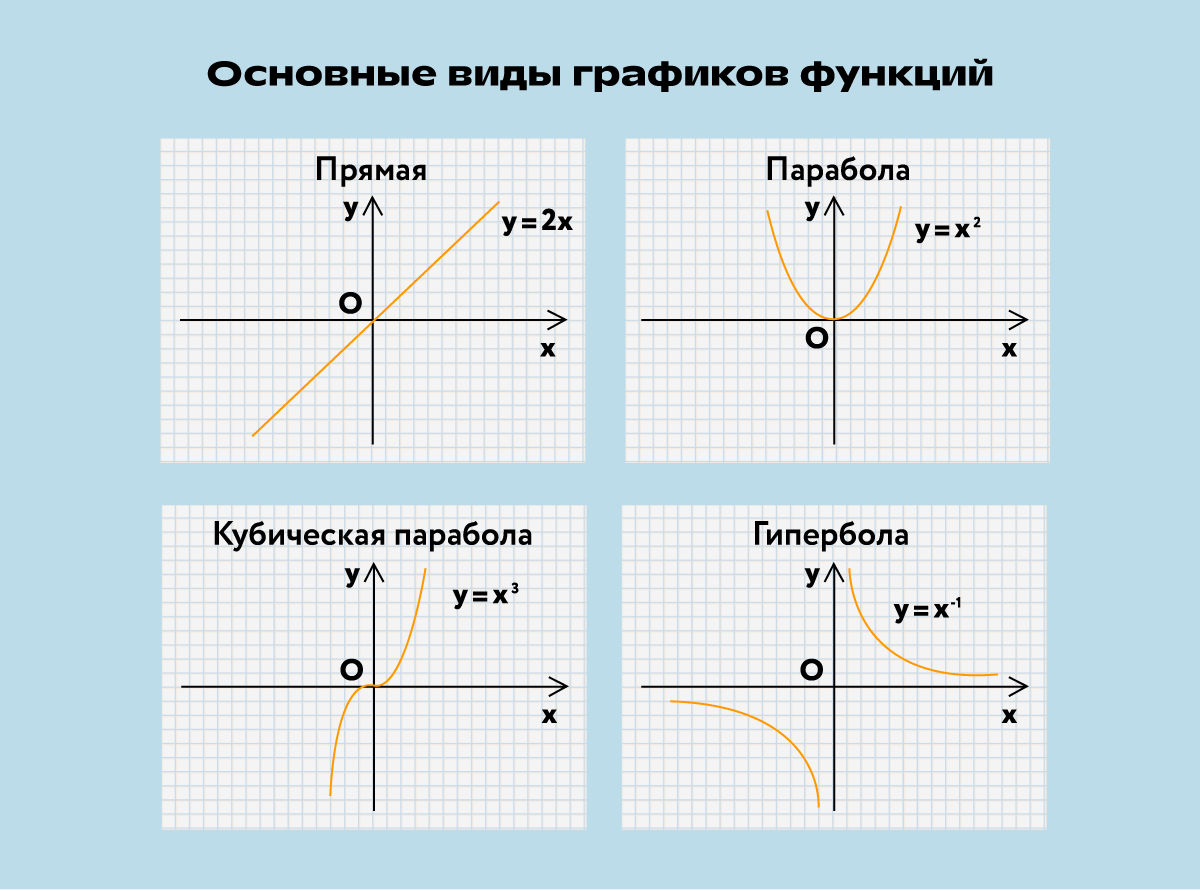
Одно из таких свойств — вид функции, например: линейная, квадратичная или тригонометрическая. Для каждого вида характерна определённая форма графика:
- для линейной — прямая линия;
- для квадратичной — парабола, или кривая в виде буквы U;
- для дробной — гипербола, состоящая из двух отдельных кривых;
- для тригонометрической — волнистые повторяющиеся кривые или серии изогнутых линий.
Исследование помогает быстро и правильно построить график, заранее представив себе его форму.
Как исследовать функцию
Чтобы выполнить исследование функции и построение графика, определяют следующие её свойства:
- Область определения — включает все возможные значения переменной x. В системе координат это те области оси Ox, где может проходить график.
- Область значений — включает все возможные значения y. Это те области оси Oy, где будет проходить график.
- Нули функции — пересечения графика с осью Ox. Чтобы найти их, вместо y подставляют 0, а затем вычисляют x.
- Убывание и возрастание — такие промежутки x, на которых y убывает (линия на координатной плоскости идёт вправо вниз) и возрастает (линия идёт вправо вверх).
- Промежутки знакопостоянства — промежутки графика, лежащие выше или ниже оси Ox. Определяются как промежутки значений x, при которых y сохраняет положительный или отрицательный знак.
График построения функции начинается с создания черновика. На нём отражают каждое из выявленных свойств: какой будет область определения и значений, где линия будет пересекаться с Ox и Oy, возрастать или убывать, идти выше или ниже оси Oy. Всё это поможет решить задачу.
Свойства функций
Важно не только знать, как исследовать функции и строить графики, но и понимать, на что влияют её свойства.
Область определения
Она ограничена всеми возможными значениями x. При некоторых условиях x перестаёт существовать. Они связаны с наличием в формуле корня, дроби и логарифма, а также арксинуса, арккосинуса, тангенса и котангенса.
Для формул с корнем нужно исключить такие x, при которых подкоренное выражение перестаёт быть положительным. Под корнем не может быть отрицательное число.
Если формула — это дробь с x в знаменателе, то нужно исключить такие значения x, при которых в знаменателе будет ноль.
Для формул с логарифмом logₐ b нужно исключить все x, при которых a или b становится отрицательным, а также x, при которых a = 1.
Для некоторых тригонометрических функций нужно исключить точки, которые находят по отдельным формулам:
- для tg (α (x)) исключают x, равные π/2 + πk (k — любое целое число);
- для ctg (α (x)) исключают x, равные πk (k — любое целое число);
- для arcsin (α (x)) и arccos (α (x)) область определения — множество чисел от –1 до 1.
Если выявлено не одно, а два или больше ограничений, например, это дробь с тангенсом в знаменателе, то нужно учесть их все для получения области определения.
Область значений и непрерывность
Все возможные значения y формируют область значений. Например, синус и косинус в составе тригонометрических формул принимают значения в интервале от –1 до 1. Это будет ограничивать область значений.
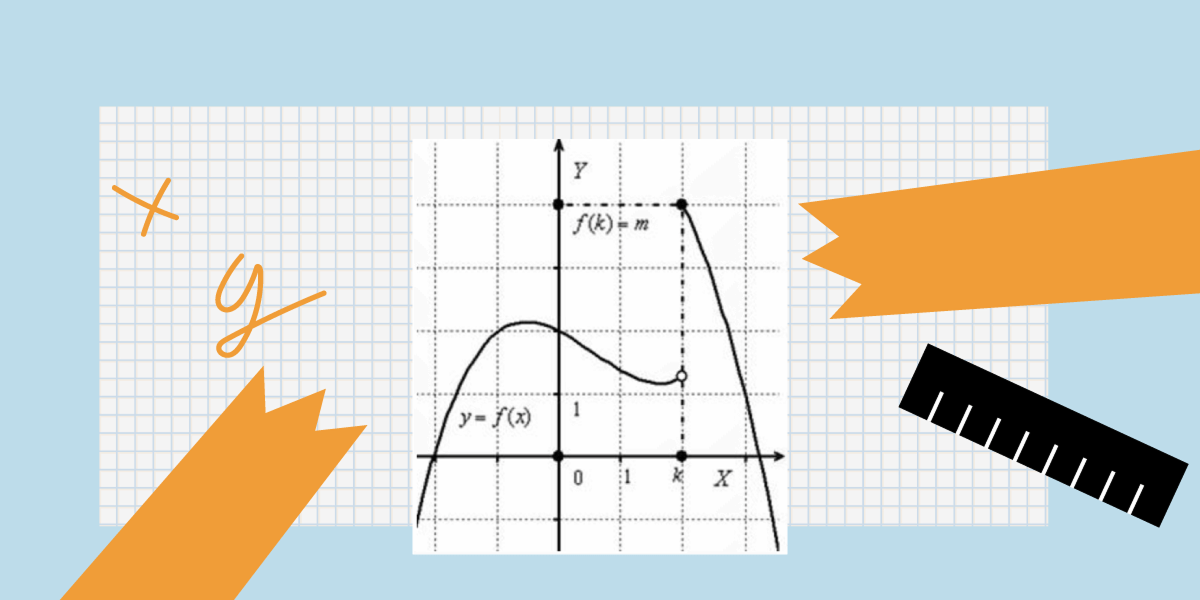
Важное свойство — непрерывность. Функция считается непрерывной, если её значения изменяются без резких скачков, плавно. Резкое изменение называется разрывом. Чаще всего это выглядит как резкий скачок линии по оси Oy с появлением «пустого» пространства между точками разрыва. Одну из них «выкалывают», то есть изображают на графике пустой, поскольку два разных y не могут соответствовать одному и тому же x.
Периодичность, чётность, нечётность
Чётность, нечётность и периодичность — свойства, которые упрощают графическое представление функции.
Периодичность означает, что для функции верно равенство f (x + T) = f (x), где T — это период, или сдвиг по оси Ox. Графиком будет кривая, повторяющаяся по оси Ox с определённым периодом. Достаточно исследования и построения кривой только в одном периоде — затем можно просто повторять её.
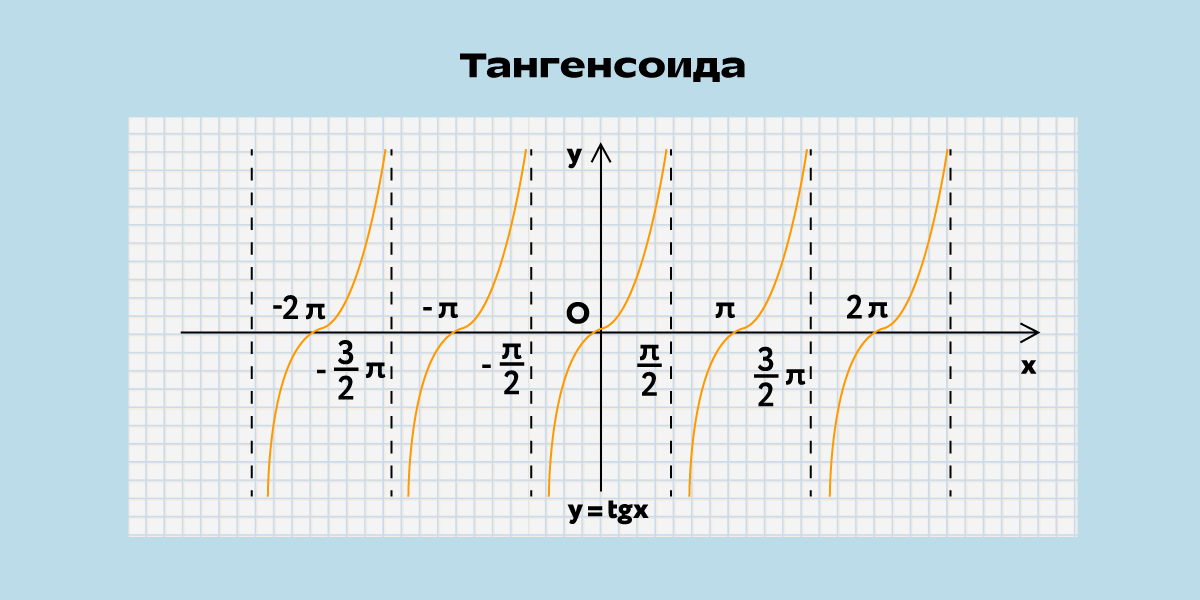
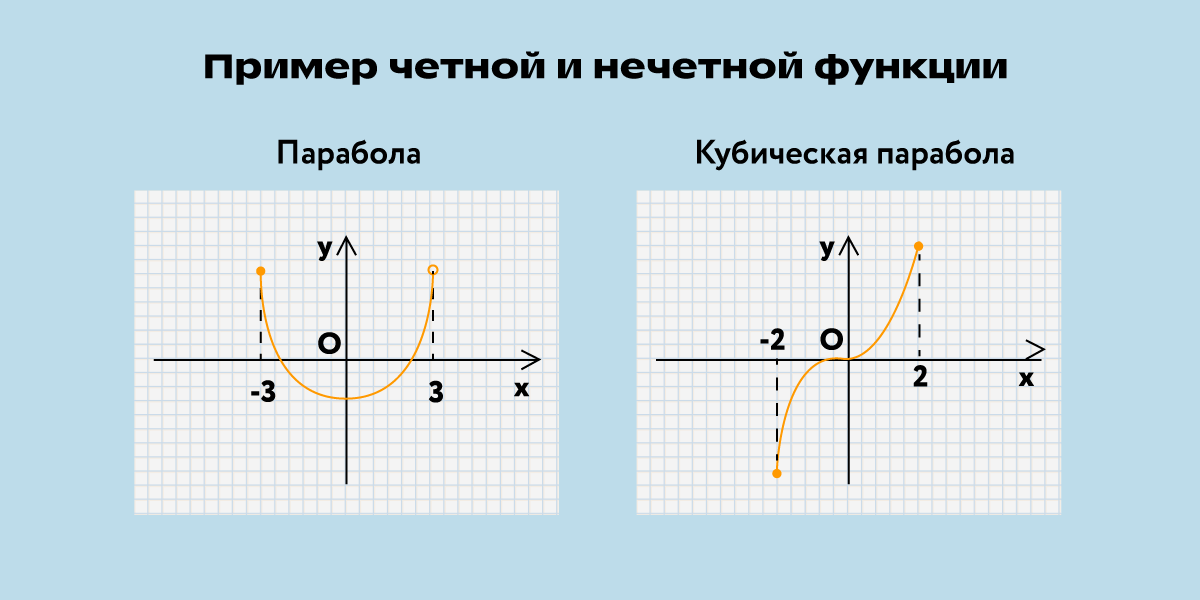
Если функция чётная, то для неё верно f (–x)= f (x). Особенность графика в его симметрии относительно оси Oy. Для нечётной верно f (–x) = –f (x). График будет симметричным относительно начала координат. В обоих случаях достаточно построить только одну часть, а затем отразить её.
Возрастание, убывание и экстремумы
На определённых участках функция может возрастать или убывать, y будет увеличиваться или уменьшаться по мере того, как увеличивается x. Это возможно как для всей области определения, так и на определённом промежутке.
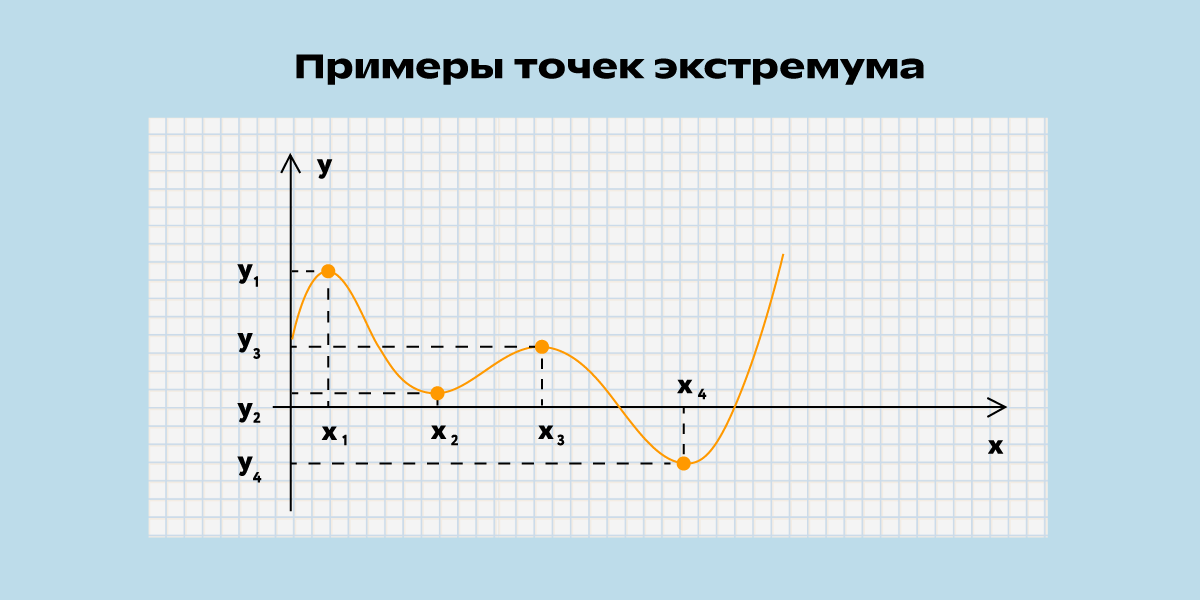
Экстремумы — максимальные и минимальные значения функции для выбранного промежутка. В графическом представлении это обычно точки, где возрастание сменяется убыванием или наоборот (но не всегда).
Основные способы построения графиков функций
Алгоритм построения графика функции не зависит от её типа. В то же время, зная тип функции, проще представить её графически.
Алгоритм построения графика линейной функции
Линейные функции считаются самыми простыми, ведь их графики выглядят как прямые. График строят всего по двум точкам. Чтобы найти их, подставьте два произвольных значения вместо x — это будут координаты по оси Ox. Получившиеся y — это координаты по оси Oy. Отметьте точки и проведите через них прямую.
Построение графика квадратичной функции
Графиком квадратичной функции будет парабола. Для y = ax2 + bx + c построить её можно за пять шагов:
- Найдите вершину. Координата x равна –b/2a. Чтобы вычислить y, подставьте полученное значение x в формулу. Через вершину проведите вертикальную ось симметрии.
- По коэффициенту A определите, будут ли ветви параболы направлены вверх (если A положительный) или вниз (если A отрицательный).
- Определите, есть ли пересечения с осью Ox. Для этого рассчитайте x при y = 0. Если такие x существуют, поставьте точки на оси Ox.
- Найдите пересечение с осью Oy. Для этого найдите y при x = 0.
- Соедините точки плавной линией.
Если нужна более высокая точность, найдите дополнительные точки.
Как строить график функции с модулем
Модуль — это абсолютное значение числа.
Это обозначение убирает возможный знак минус у выражения внутри прямых скобок. График может проходить только выше оси Ox или правее оси Oy, в зависимости от того, какое выражение поместили под знак модуля. Например, для y = |x| нужно начертить две прямые: y = x и y = –x, оставив только те их участки, что лежат выше оси Ox.
Другие виды функций
Большая группа функций — степенные. Их графики как будто состоят из «половинок» параболы, развёрнутых разным образом. Например, у кубической параболы ветвь, находящаяся левее вершины, развёрнута вниз из-за того, что степень нечётная. Если x отрицательный, y тоже будет отрицательным.
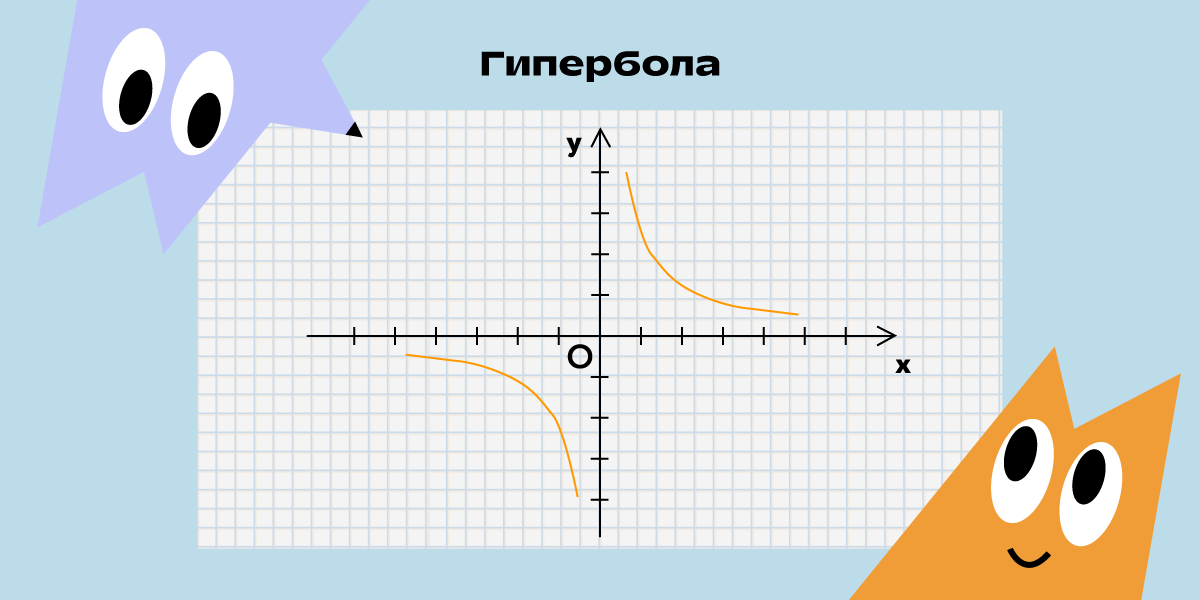
Если в формуле дробное выражение с x, графически она будет иметь вид гиперболы. Она состоит из двух непересекающихся ветвей с разрывом между экстремумами.
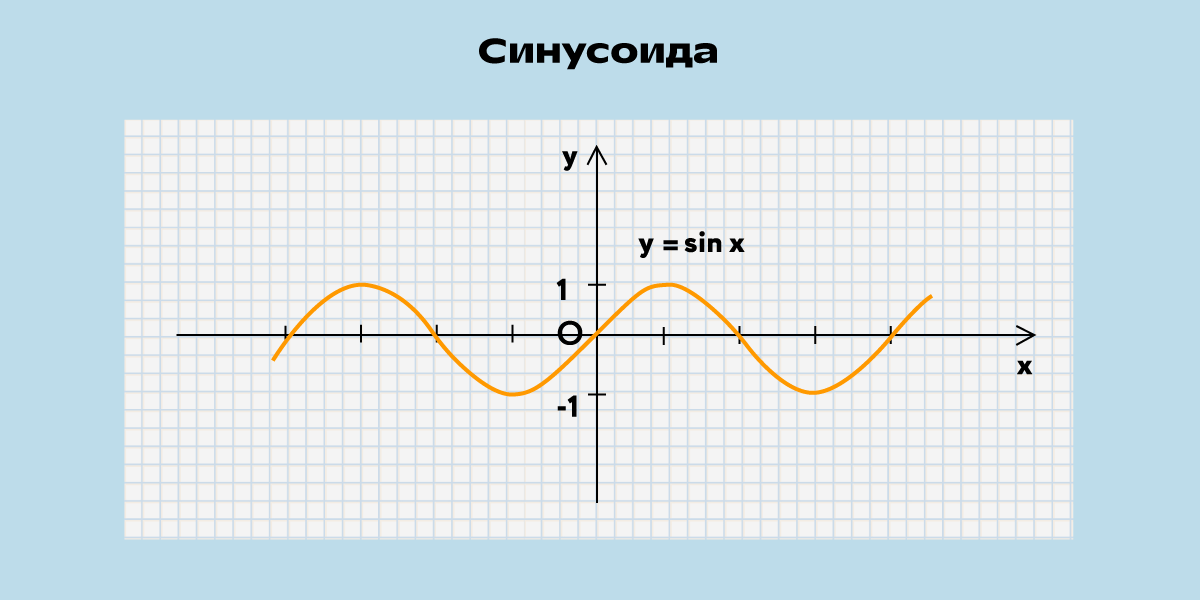
Тригонометрические функции всегда периодичны — то есть график будет повторяться на определённом интервале.
Построение графиков сложных функций
В таких случаях нужно пошаговое и полное исследование функции и построение графика:
- Сначала выявите основные свойства: ограничения области определения и значений, чётность, нечётность, периодичность и точки разрыва.
- Вычислите, есть ли пересечения с Ox и Oy и где они (при y = 0 и x = 0). Отметьте интервалы знакопостоянства. Найдите минимумы и максимумы.
- Если выполняется построение графика функции с помощью производной, найдите её с помощью подходящей формулы. Интервалы, на которых производная окажется положительной, — это интервалы возрастания функции, и наоборот.
- Составьте таблицу с дополнительными значениями x и y, если нужно повысить точность.
Отметьте точки, соедините их плавной линией — и график готов.
Примеры функций и графиков
Линейная функция
Достаточно вычислить координаты любых двух точек.
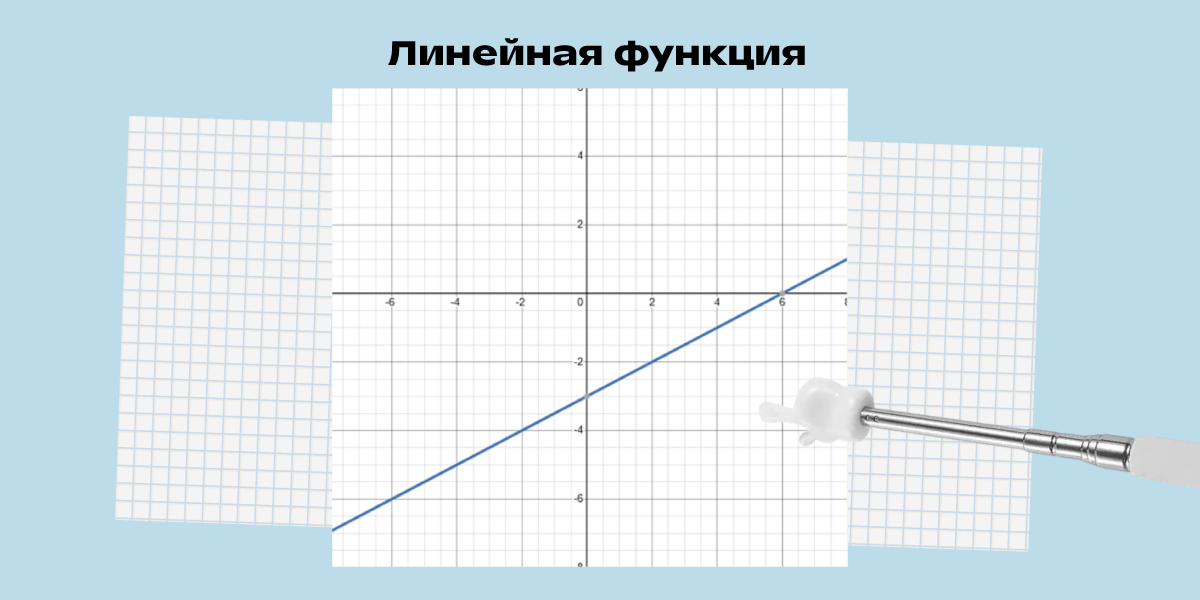
Для y = 0,5x – 3 можно найти пересечения с Ox и Oy:
- 0 = 0,5x – 3 — точка А (6; 0);
- y = 0,5 * 0 – 2 — точка B (0; –3).
Квадратичная функция
Нужно построить параболу.
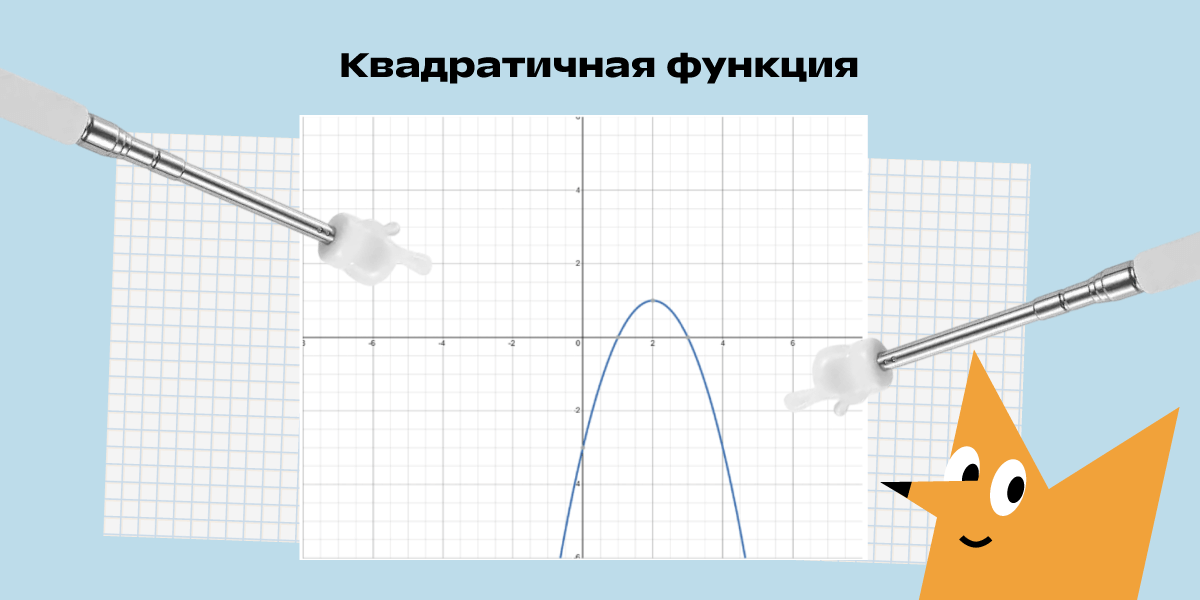
Для y = –x2 + 4x – 3 находим точки:
- вершина x0 = –4/(2 –1) = 2, y0 = –1 * 22 + 4 * 2 – 3 = 1 — точка C (2; 1);
- лежащие на Ox: 0 = –x2 + 4x – 3 — A (1; 0), B (3; 0);
- лежащие на Oy: y = –02 + 4*0 – 3 — точка D (0; –3).
Парабола симметрична, а значит, правая ветвь будет отражением левой.
Дробно-рациональная функция
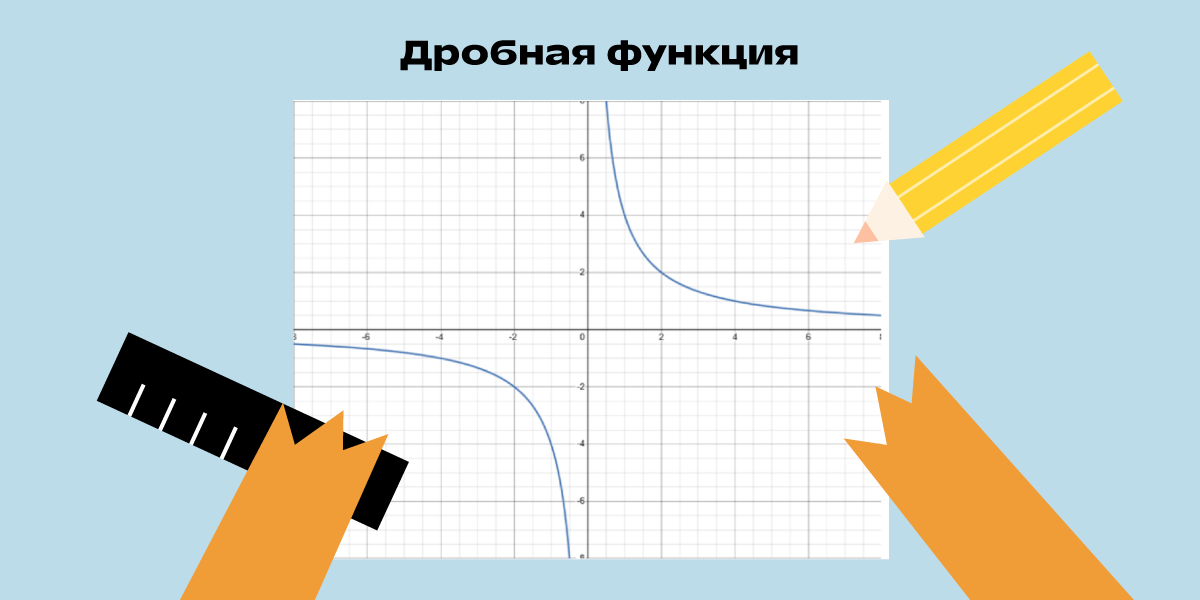
Нужно построить гиперболу, и для этого находят несколько произвольных точек, подставляя значения x в формулу. Например, для y = 4/x достаточно 6 точек:
- A (–4; –1);
- B (–2; –2);
- C (–1; –4);
- D (1; 4);
- E (2; 2);
- F (4; 1).
Графики функций помогают представлять формулы и лучше понимать их. Их построение — удобный способ решения математических задач. Его не так трудно освоить: достаточно попрактиковаться, постепенно переходя от простых заданий к более сложным.
Ответим на ваши вопросы
Свяжемся с вами в течение 5 минут и проведём бесплатную консультацию по вопросам перехода на домашнее обучение
Позвоним с 8 до 21 в рабочие дни






