Что такое дроби и почему они важны
Прежде чем объяснить ребёнку тему «Дроби», убедитесь, что он уверенно владеет базовыми математическими операциями с целыми числами. Это как изучение языка: без знания алфавита сложно читать книги.
Большинство детей воспринимают дроби как нечто абстрактное и непонятное. Они привыкли к целым числам — 1, 2, 3, где всё ясно и конкретно. А тут вдруг появляются какие-то чёрточки, числители и знаменатели. Исследователи выяснили, что переход к дробям требует «концептуальной перестройки» числового мышления.
Начните с простого определения: дробь — это часть чего-то целого. Это «что-то» может быть любым предметом, который можно разделить: яблоком, пиццей, плиткой шоколада или даже временем. Помните мультфильм про апельсин? «Мы делили апельсин, много нас, а он один...» — это и есть наглядная демонстрация принципа дробления.

Важно донести до ребёнка, что дроби — это не просто школьное задание, а инструмент для понимания мира. Они помогают:
- точно рассчитывать количество ингредиентов в кулинарии;
- понимать время и планировать день;
- делить игрушки справедливо;
- понимать скидки в магазинах;
- измерять расстояния и размеры.
Когда ребёнок осознаёт практическую ценность дробей, изучение становится осмысленным и интересным.
Наглядное объяснение дробей
Объяснение дробей с помощью конструктора Lego
Этот метод особенно эффективен, потому что дети воспринимают занятие как игру:
- Составление фигур: попросите собрать конструкцию с 10 выступающими шипами из 5 деталей (используя блоки по 2 шипа каждый).
- Поиск половины: создайте фигуру с 8 шипами, попросите показать половину (4 шипа). Объясните, что 4/8 — это то же самое, что 1/2.
- Сложение дробей: пусть ребёнок к 3/4 блока добавит 2/8 и посмотрит, что получилось.
Циферблат часов как пример целого числа
Круглый циферблат отлично подходит для визуализации дробей:
- Разделите циферблат пополам вертикальной линией — покажите 1/2.
- Добавьте горизонтальную линию — получится 4 части, изучайте 1/4, 3/4.
- Используйте 12 делений циферблата для изучения дробей со знаменателем 12.
Бонус: ребёнок заодно лучше научится определять время по часам.
Цветная бумага и аппликации для наглядности при дроблении
Нарежьте полоски бумаги разных цветов одинаковой длины:
- красную оставьте целой;
- жёлтую разрежьте на 2 части;
- синюю — на 4 части;
- зелёную — на 8 частей.
Попросите ребёнка показать 1/2, 3/4, 5/8, сравнить разные дроби между собой.
Из чего состоит дробь
Когда ребёнок поймёт суть деления на части, можно познакомить его с математической записью. Обыкновенная дробь выглядит как «двухэтажное» число: два числа, разделённые горизонтальной чертой.
Верхний «этаж» — числитель, он показывает, сколько частей мы взяли.
Нижний «этаж» — знаменатель, он говорит о том, на сколько частей разделили целое.
Как проще объяснить ребёнку дроби? Отправляйтесь на кухню! Если торт разрезали на 8 кусков, а Маша съела 3 из них, то запись будет выглядеть так: 3/8. Знаменатель (8) показывает общее количество кусков, а числитель (3) — сколько кусков торта съела Маша.
Важные правила, которые нужно запомнить:
- Дробь всегда меньше целого числа — логично, ведь это только часть чего-то целого.
- Чем больше частей, тем они меньше — каждый кусочек торта, разделённого на восемь человек, меньше, чем каждый кусочек того же торта, разделённого на четырёх человек.
- Дробная черта означает деление — это важно помнить для дальнейших вычислений.
Как правильно читать дроби
Объясните ребёнку систему вопросов:
- Числитель отвечает на вопрос «сколько?».
- Знаменатель отвечает на вопрос «каких?» или «какая?».
В примере 1/10 читаем: «Одна десятая». Если возьмём 3 квадратика, получится 3/10 — «три десятых».
Правильные и неправильные дроби
Когда ребёнок разберётся с основами, можно объяснить ему примеры с дробями разных типов. В правильных дробях числитель меньше знаменателя (как 3/8), а в неправильных — больше или равен ему (как 9/8).
Представьте ситуацию: мама приготовила два одинаковых пирога для семейного ужина и разрезала каждый на 6 кусков. Папа очень любит мамину выпечку и съел 10 кусочков из всех имеющихся. Как это записать? 10/6 — это и есть неправильная дробь.
Смешанные дроби
Когда основы усвоены, можно переходить к более сложным концепциям — смешанным дробям, у которых есть целая и дробная часть.
Начнём с самых лёгких примеров. Представьте, что у нас есть дробь 12/4. Что произойдёт, если мы разделим 12 на 4? Получится ровно 3 — никаких остатков. Аналогично с дробью 15/5: при делении получаем чистое число 3.
Эти случаи похожи на ситуацию, когда вы делите между детьми поровну конфеты, и они распределяются без остатка. Каждый получает одинаковое количество, и никого не нужно расстраивать.
А теперь рассмотрим более интересный случай. Возьмём дробь 11/3 и попробуем выяснить, что она означает на самом деле.
Выполняем деление: 11 разделить на 3. Сколько троек помещается в числе 11? Правильно, три тройки (3 × 3 = 9), но при этом остаётся ещё 2 единицы (11 – 9 = 2).
Получается 11 ÷ 3 = 3 с остатком 2.
Как убедиться, что мы всё сделали правильно? Применим обратную операцию:
3 (целые части) × 3 (знаменатель) + 2 (остаток) = 9 + 2 = 11. Всё сходится. Значит, наши вычисления верны.
Теперь самое важное — красиво и понятно записать результат. Полученное число состоит из двух компонентов:
- целой части — это 3 (количество полных групп);
- Дробной части — это 2/3 (остаток, записанный как дробь).
Итоговая запись выглядит как 3 ⅔ и читается «три целых две третьих». Это действие ещё называется «выделение целой части».
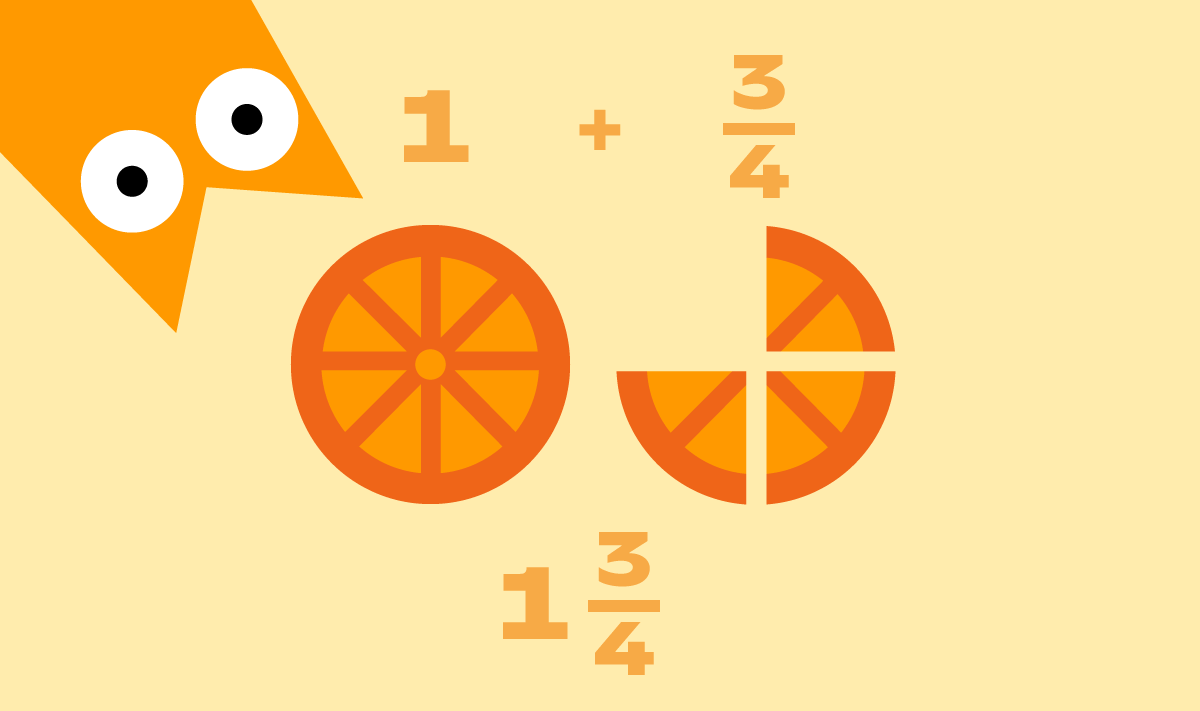
Как объяснить ребёнку десятичные дроби
Объяснить ребёнку десятичные дроби проще всего, опираясь на знакомые обыкновенные дроби:
- Покажите, что 4 целых 3/10 можно записать как 4,3.
- Объясните правило: сколько нулей в знаменателе, столько цифр после запятой.
- Тренируйтесь на примерах: 5/100 = 0,05, 8/1 000 = 0,008.
Используйте деньги как наглядный пример: 50 копеек — это 50/100 рубля, или 0,5 рубля.
Сравнение дробей с одинаковыми числителями
Многие дети думают, что 1/20 больше 1/10, потому что 20 больше 10. Покажите наглядно на двух одинаковых плитках шоколада:
- первую разделите на 10 частей;
- вторую — на 20 частей (каждый кусочек ещё пополам);
- пусть ребёнок сравнит размер 1/10 и 1/20.
Правило запомнится навсегда: чем больше частей, тем они меньше.
Операции с дробями
Сложение и вычитание дробей с одинаковыми знаменателями объясните с помощью апельсина:
- было 10/10 долек (целый апельсин);
- 3/10 съели — осталось 7/10;
- 1/10 вернули — стало 8/10.
Покажите, что складываются и вычитаются только числители, знаменатель остаётся прежним.
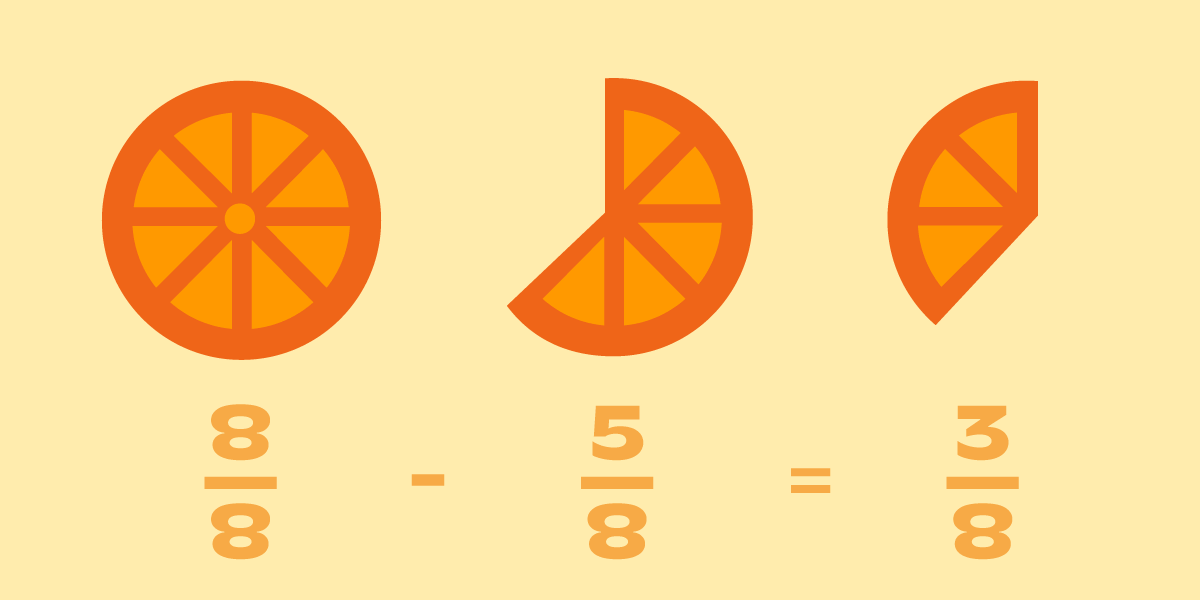
Когда обращаться за дополнительной помощью
Иногда, несмотря на все усилия, дроби остаются тёмным лесом. Не стесняйтесь обратиться к учителю или репетитору. Возможно, ребёнку нужен другой подход или дополнительная практика.
Помните: каждый ребёнок уникален и то, что подходит одному, может не сработать для другого. Главное — сохранять терпение, поддерживать интерес к математике и показывать, что дроби — не враги, а полезные инструменты для понимания мира вокруг нас.
Резюме
Объяснить ребёнку дроби — задача выполнимая. С правильным подходом, наглядными примерами и достаточным количеством практики ваш школьник не только поймёт эту тему, но и скорее полюбит математику. Ведь нет ничего лучше момента, когда в глазах ребёнка загорается огонёк понимания: «А, так вот как это работает!»
Ответим на ваши вопросы
Свяжемся с вами в течение 5 минут и проведём бесплатную консультацию по вопросам перехода на домашнее обучение
Позвоним с 8 до 21 в рабочие дни






